Classificação de equações lineares.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

Qualquer equação linear, depois de simplificada, pode ser escrita na forma `ax=b`, onde `a` e `b` são números racionais. A resolução desta equação pode originar três tipos de soluções distintas:
Equação Impossível: Por exemplo, `0x=5`. (Não existe nenhum número que multiplicado por zero vá dar cinco).
Logo, podemos definir uma equação impossível, como como sendo aquela
em que não há nenhum valor de `x` que satisfaça a igualdade, ou, por outras palavras, a igualdade é falsa.
Equação Indeterminada: Por exemplo, `0x=0`. (Qualquer número multiplicado por zero vai dar zero).
Assim sendo, podemos definir uma equação indeterminada, como sendo aquela em que a igualdade se vai verificar, qualquer que seja o valor de `x`.
Equação Possível e Determinada: Por exemplo, `2x=12`. (O único número que multiplicado por dois vai dar doze é o número seis).
Por último, podemos definir uma equação possível e determinada, como sendo uma equação em que existe, pelo menos, um valor de `x` que torne a igualdade verdadeira.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
18 de Outubro de 2023, 19h08
Mensagem de Roberto
No exercicio nº3 na alinia a) o resultado nao deveria ser -2 ? Tendo em conta que o 5 quando passa para o outro lado a dividir também tem de trocar o sinal ?
19 de Outubro de 2023, 07h55
Mensagem de Vitor
Olá Roberto,
Repara que nesse exercício o número 5 está a multiplicar pelo `x`. Quando passa para o segundo membro, passa a dividir. Mas, nestes casos, não há troca de sinal. Só existe lugar a troca de sinal, quando se está a somar e passa para o outro membro a subtrair ou vice-versa. Espero ter ajudado!
21 de Fevereiro de 2024, 12h00
Mensagem de João Cordeiro
Olá. Como sempre, o vosso curso continua muito bom.
A título de sugestão, no intuito de contribuir para o curso, eu sugiro que se defina equação impossível como como sendo aquela em que não há nenhum valor de x que satisfaça a igualdade, ou, em outra palavras, a igualdade é falsa; e equação indeterminada como sendo aquela em que a igualdade vai se verificar, qualquer que seja o valor de x. O que acha?
22 de Fevereiro de 2024, 08h06
Mensagem de Vitor Nunes
Olá João,
Agradeço as palavras amáveis, bem como a sugestão. A introdução da aula já foi alterada, de acordo com as suas recomendações. Obrigado!
07 de Abril de 2024, 10h13
Mensagem de Maria
Olá!
Tenho de lhe felicitar pelo o site! É um ótimo recurso para não só treinar com exercícios, mas também para compreender a matéria.
Estou dificuldades na resolução deste problema... podia-me ajudar?
O perímetro de um retângulo é 22 cm. Sabe-se que a diferença entre o comprimento e a largura desse retângulo é 5 cm. Determina a área do retângulo.
Obrigada e felicidades
08 de Abril de 2024, 08h47
Mensagem de Vitor Nunes
Olá Maria,
Vamos supor que o comprimento é `x`, neste caso como a diferença entre o comprimento e a largura é de 5 cm, então a largura pode ser dada por `x-5`. Posto isto, o perímetro pode ser calculado pela soma de todos os lados. Assim sendo, o perímetro é igual a `2x+2(x-5)`. Como o enunciado nos diz que o perímetro é igual a 22 cm, podemos igualar a expressão anterior a 22. Assim vamos obter equação `2x+2(x-5)=22`. Como a resolução desta equação é acessível, deixo-te o trabalho de a resolver, penso que não deverá ser difícil chegar ao resultado final. Assim que ficares a conhecer o valor de `x` que se refere ao comprimento, chegas facilmente à largura e por fim, para encontrar a área é só multiplicar o comprimento pela largura. Bons cálculos!

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.
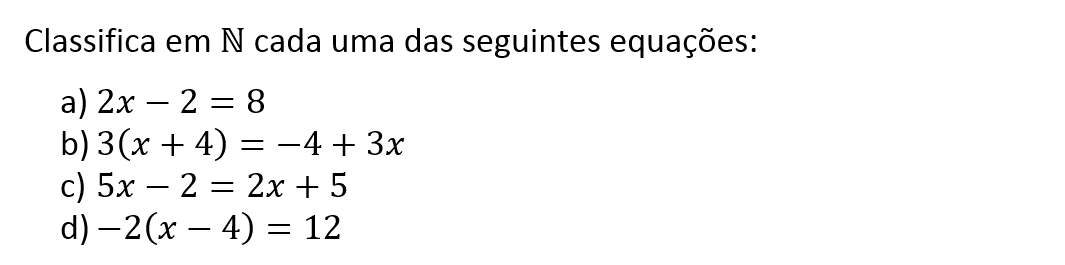

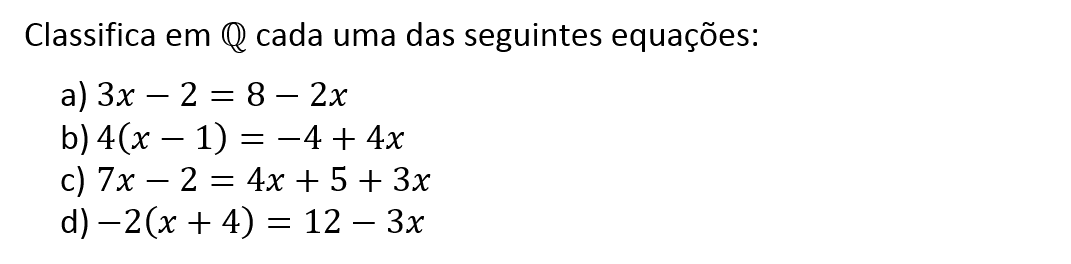

 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 