Assíntotas e domínio das funções racionais.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

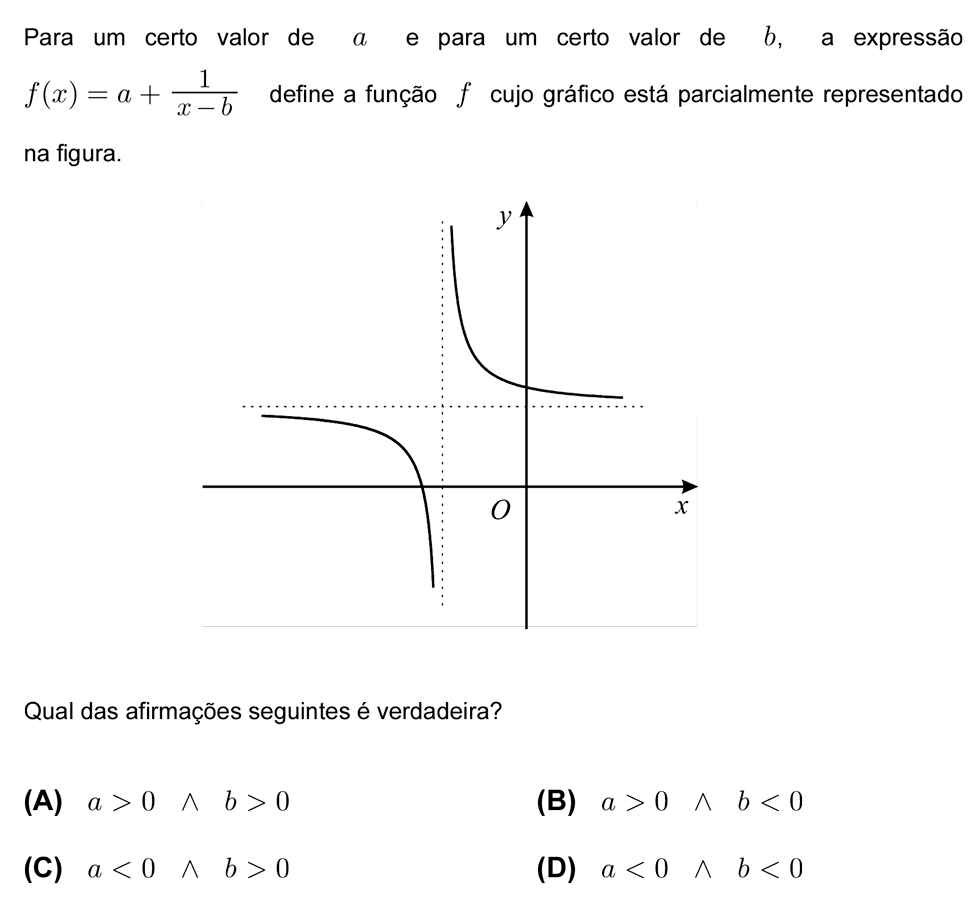
Funções do tipo `f(x) = b + a/(x-c)` :
Domínio: `Rtext(\){c}` Contradomínio: `R text(\){b}`
Assíntota Vertical: `x =c` Assíntota Horizontal: `y =b`
Funções do tipo `f(x) = (ax + b)/(cx + d)` :
Domínio: `R text(\){-d/c}` Contradomínio: `R text(\){a/c}`
Assíntota Vertical: `x =-d/c` Assíntota Horizontal: `y =a/c`
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
29 de Janeiro de 2016, 23h28
Mensagem de Bia
Olá, gostaria de saber quando o Domínio é IR, qual a representação gráfica da função .
01 de Fevereiro de 2016, 13h15
Mensagem de Vitor Nunes
Olá Bia,
Em relação às funções racionais que estão aqui a ser estudadas o Domínio dessas funções nunca é `RR`. Isto porque, estas funções contém sempre uma assíntota vertical, logo nesse ponto a função não está definida. Espero ter ajudado!
23 de Fevereiro de 2016, 23h09
Mensagem de Maria
Olá, gostaria de saber de que forma é possível passar da expressão f(x)=b+(a/(x-c)) para a expressão f(x)=(ax+b)/(cx+d)?
Obrigada desde já e parabéns pelo ótimo trabalho!
24 de Fevereiro de 2016, 08h43
Mensagem de Vitor Nunes
Olá Maria,
Normalmente, aquilo que se pretende é o inverso! Mas se for mesmo isso que pretendes, basta colocar o mesmo denominador na constante `b` (multiplicando e dividindo por `x-c`) e depois juntar as duas frações numa só. Se o que pretendes é o oposto, então faz-se a divisão dos polinómios `ax+b` por `cx+d` e aplica-se a seguinte fórmula: `D/d = q + r/d` (`D`: Dividendo; `d`: divisor; `q`: quociente; `r`: resto).
06 de Maio de 2016, 19h04
Mensagem de Ana
Olá, tenho um dúvida se simplificarmos a expressão (x^2+x-2)/(x^2+2x) obtemos (x-1)/x. Contudo o domínio da primeira é IR/{-2,0} e o domínio da segunda é IR/{0}, não deviam de ter o mesmo domínio visto que a segunda é a versão simplificada da primeira?
08 de Maio de 2016, 17h18
Mensagem de Vitor Nunes
Olá Ana,
Essa é uma dúvida comum e a resposta é não. Para caracterizar uma função é necessário conhecer o seu domínio e o processo que permite determinar a imagem de qualquer elemento do seu domínio. Isto porque, duas funções `f` e `g` dizem-se iguais (ou idênticas) se e só se tiverem o mesmo domínio e se `f(x)=g(x)`. No teu exemplo, apesar das duas funções terem a mesma lei de transformação (ou expressão analítica) possuem domínios diferentes. Logo não são iguais. Não se pode dizer que a segunda é uma "versão simplificada" da primeira. Tal coisa, não existe na matemática!
27 de Maio de 2016, 11h17
Mensagem de Patrícia
Então e se a expressão for f(x)=(ax+b)/(cx-d), ou seja, não estiver na forma padrão, há o menos (-) no denominador, é como se fosse f(x)=(ax+b)/(cx+(-d))? E a assintota vertical seria: -(-d)/c = d/c? Obrigada.
29 de Maio de 2016, 07h28
Mensagem de Vitor Nunes
Olá Patrícia,
Exatamente. Se a constante `d` for negativa procede-se do modo que indicas. Aliás se qualquer das constantes for negativa utiliza-se um raciocínio análogo ao que indicaste. Boa sorte para os exames!
26 de Março de 2017, 13h37
Mensagem de Ana
Olá, gostaria de saber qual é o domínio e como se simplifica f(x)= 2x^3 + 5x^2 +x-2/ x^2+x.
26 de Março de 2017, 15h44
Mensagem de Vitor Nunes
Olá Ana,
Não tenho por hábito responder a questões sobre exercícios que não estejam no site. Posso, no entanto, dar algumas indicações que te indiquem o caminho. Em relação ao Domínio da função basta averiguar quando é que o denominador é diferente de zero, ou seja, `x^2+x != 0`. Quanto à simplificação, investiga quais são os zeros do numerador e os zeros do denominador, se por acaso tiverem algum zero em comum, então é possível simplificar a função. Sugestão: usando a Regra de Ruffini verifica se é possível dividir o numerador por `(x+1)`.
08 de Maio de 2024, 18h45
Mensagem de Alexandre
No ex.9 não se resolveu a monotonia?
09 de Maio de 2024, 10h29
Mensagem de Vitor Nunes
Olá Alexandre,
O enunciado do exercício só pede que seja estudado o domínio, o contradomínio e as equações das assíntotas. Não é solicitado que se faça o estudo da monotonia das funções.

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.






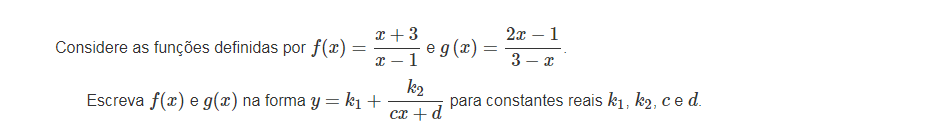




 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 