Operações com funções: soma, diferença, produto e quociente. Função composta.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

No estudo das funções reais de variável real, deves ter presente que, para caracterizar, ou seja, definir uma função, é necessário conhecer o seu domínio e o processo que permite determinar a imagem de qualquer elemento do domínio (lei de transformação).
Duas funções `f` e `g` dizem-se iguais (ou idênticas), escrevendo `f=g`, se e só se, tiverem o mesmo domínio e se as imagens das duas funções forem iguais para qualquer objeto pertencente ao seu domínio.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
08 de Abril de 2015, 15h50
Mensagem de Alex
No exercicio nº 5 a resposta certa, não deveria ser a opção A)? Porque são 5 zeros da função f + 3 zeros da função g e como um deles está repetido subtraímos 1. Assim 5+3-1=7. Pelo menos é assim que eu pensava que se contava os zeros de uma função.
09 de Abril de 2015, 11h03
Mensagem de Vitor Nunes
Olá Alex,
O raciocínio está correto, mas estás a esquecer-te de um pormenor: a função `g` está no denominador e portanto nenhum dos seus zeros pode ser contabilizado. Como um dos zeros da função `f` é comum aos zeros da função `g` temos também que "descontar" esse. Se vires o vídeo, essa situação está bem explicada.
Boa sorte para os testes!
01 de Abril de 2016, 11h40
Mensagem de IML
Olá. Não percebi o exercicio 5.
Obrigada pela ajuda que o site fornece.
04 de Abril de 2016, 08h38
Mensagem de Vitor Nunes
Olá Inês,
Como não dás detalhes, não consigo saber qual é a tua dúvida. Não sei se leste a minha resposta anterior, nela explico que para descobrir os zeros da função `f/g` temos que primeiro descobrir os zeros da função `f`, depois encontrar os zeros da função `g`. Por fim, devemos lembrar-nos que a função `g` está no denominador logo `f = 0 ^^ g != 0`. Por este motivo, se houver zeros comuns entre as duas funções temos que retirar da contagem os zeros da função `g`. Espero ter ajudado!
05 de Fevereiro de 2017, 21h19
Mensagem de Cat
Boa noite.
Surgiu-me uma dúvida no ex.8.
Quando se vai calcular o objeto cuja imagem é 1/9 qual a razão de se usar a função g e não a função h? Quando temos exercícios deste tipo utiliza-se sempre a função que em 1º lugar (neste caso a g)? Obrigada
06 de Fevereiro de 2017, 08h41
Mensagem de Vitor Nunes
Olá Cat,
Neste tipo de exercício de função composta, se nos fosse dado o objeto e pretendêssemos obter a imagem, então utilizaríamos primeiro a segunda função e só depois aquela que vem em primeiro lugar. Neste exercício com composição de funções, passa-se o oposto: dão-nos a imagem e pretende-se descobrir o objeto. Assim sendo, faz-se ao contrário, utiliza-se primeiro a função que aparece em primeiro lugar e só depois disso é que se usa a segunda função. Espero ter ajudado!
06 de Fevereiro de 2017, 15h06
Mensagem de Cat
Sim, ajudou e muito!! Obrigada pela explicação professor e continuação de boas explicações!
20 de Novembro de 2017, 17h15
Mensagem de Cat
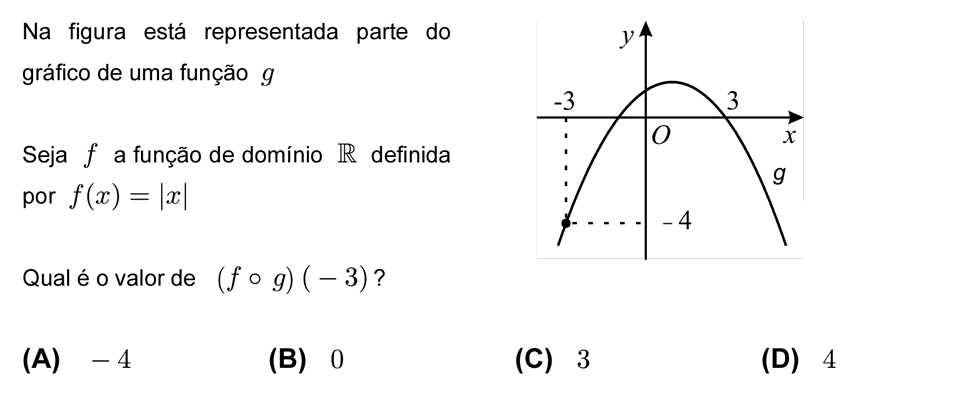
Como posso determinar os zeros de uma função composta (gof), se tiver a expressão de f e apenas o gráfico e domínio de g?
20 de Novembro de 2017, 17h48
Mensagem de Duarte
Boa noite! Como é que se calcula o domínio de hof, se apenas tiver acesso à expressão de h e ao gráfico e domínio de f?
21 de Novembro de 2017, 11h05
Mensagem de Vitor Nunes
Olá Cat,
Para encontrar os zeros vamos começar por igualar a função composta a zero, ou seja, `g_of(x)=0 hArr g[f(x)]=0`. A partir daqui basta observar o gráfico da função `g` e verificar quais são os zeros. Vamos supor que função `g` apenas possui um zero no ponto 2, nesse caso para finalizar o exercício basta ver quando é que `f(x)=2`.
21 de Novembro de 2017, 11h36
Mensagem de Vitor Nunes
Olá Duarte,
Para calcular o domínio da função composta `h_of`, primeiro vemos o domínio da função `f`. Vamos supor que o domino de `f` é `RR`. O passo seguinte é ver o domínio da função `h`. Vamos agora supor que o domino de `h` é `RR\\{3}`. Neste exemplo, o próximo passo consiste em analisar o gráfico e verificar quando é que `f(x) != 3`.
21 de Novembro de 2017, 16h44
Mensagem de Duarte
Obrigada pelo esclarecimento e uma continuaçao do ótimo trabalho com estas aulas!
30 de Novembro de 2017, 16h22
Mensagem de Rui
Boa tarde, como posso calcular os zeros da função f-h se só tiver os gráficos de f e h? E, nas mesmas condições, calcular os zeros de f×h?
01 de Dezembro de 2017, 09h00
Mensagem de Vitor Nunes
Olá Rui,
No caso dos zeros de `fxxh` é fácil, basta utilizar a lei do anulamento do produto, que diz o seguinte: `fxxh=0 hArr f=0 vv h=0`. E assim sendo, os zeros dessa função resultam da reunião dos zeros de `f` com os zeros de `h`. Quanto aos zeros de `f-h` também não é difícil. Repara que se pretende resolver a seguinte equação `f-h=0 hArr f=h`. Logo, os zeros de `f-h` encontram-se no ponto de interseção destas duas funções. Espero ter ajudado!
23 de Julho de 2020, 14h57
Mensagem de Alix
Boa tarde, no exercício 12 os conjuntos de chegada estão errados à excepção do (f-g)(x), estou certo?
Caso contrário não entendi o porquê de ser sempre IR.
23 de Julho de 2020, 16h10
Mensagem de Vitor Nunes
Olá Alix,
Repara que contradomínio não é o mesmo que conjunto de chegada. O contradomínio de uma função corresponde a um conjunto que contém apenas as imagens da função. Por sua vez, o conjunto de chegada é um conjunto que além de conter as imagens, pode também conter outros elementos que não são imagens da função. Tendo em conta esta definição, não é incorrecto afirmar, que no exercício 12, o conjunto de chegada das diversas funções é `RR`.

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.









 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 