Segunda derivada. Aceleração e concavidade.
Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução
É frequente ouvirem-se expressões do tipo:
“… cresce mais rapidamente…”;
“… cresce cada vez mais devagar…”;
“… decresce lentamente…”.
Neste tipo de expressões está implícita a ideia de variação do crescimento ou decrescimento, que é dada pelo sinal da segunda derivada, o que, em termos gráficos, se traduz no tipo de curvatura do gráfico.
Dada uma função `f` diz-se que o ponto `P (a, f(a))` é um ponto de inflexão ao gráfico de `f`, se o sentido da concavidade muda em `P`.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
ATENÇÃO: Para poder utilizar esta opção terá que fazer Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
08 de Abril de 2015, 15h52
Mensagem de Magda
Já estive a ver a aula em vídeo e continuo sem perceber para que é que serve a segunda derivada. Porque é que temos que derivar uma função duas vezes e ir ver os seus zeros?
09 de Abril de 2015, 11h13
Mensagem de Vitor Nunes
Olá Magda,
A primeira derivada permite-nos conhecer a monotonia da função, isto é, analisando o sinal conhecemos os intervalos em que ela é crescente, decrescente ou constante. Além disso, através do cálculo dos seus zeros, conseguimos também saber se a função tem máximos ou mínimos. Por outro lado, a segunda derivada permite-nos conhecer, através da análise do sinal, o sentido da concavidade. Além disso, os Pontos de Inflexão são obtidos através do conhecimento dos zeros da segunda derivada.
Espero ter ajudado!
06 de Abril de 2016, 17h34
Mensagem de Bruno
Boa tarde, apenas queria dizer que os exercícios 13 e 20 são iguais.
Obrigado pelas explicações fantásticas, dão muitíssimo jeito. Continuação de um bom trabalho.
07 de Abril de 2016, 14h28
Mensagem de Vitor Nunes
Olá Bruno,
Tens toda a razão, já eliminei o exercício 20, uma vez que ele estava repetido. Obrigado por ter reportado o erro e agradeço também as palavras de elogio. Continuação de bons estudos!
16 de Abril de 2018, 21h18
Mensagem de Joao Vasconcelos
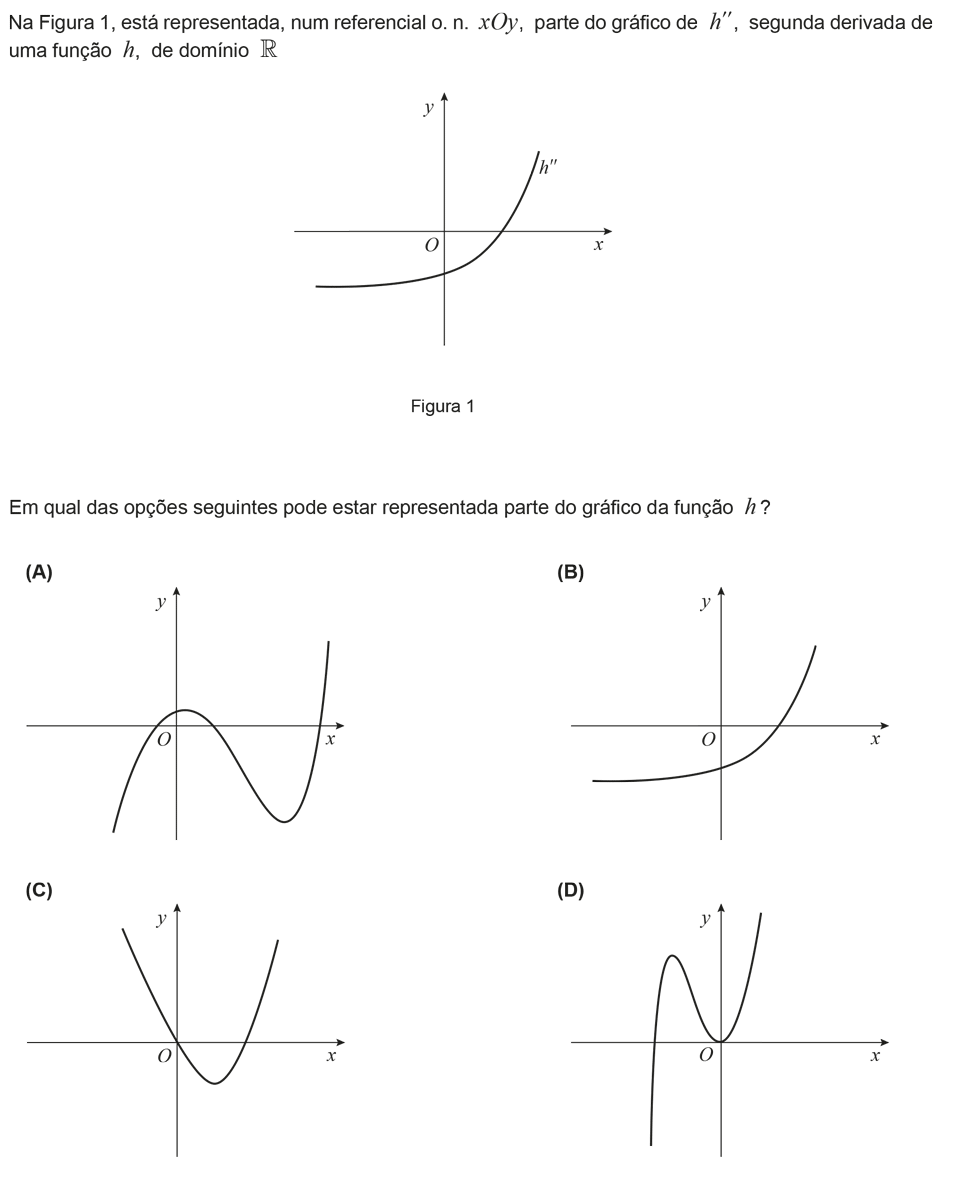
Boa noite, no exercício numero 5 a resposta D também tem a concavidade virada para cima ao início, um ponto de inflexão e depois a concavidade virada para baixo. Porque razão está a resposta D incorrecta?
17 de Abril de 2018, 08h48
Mensagem de Vitor Nunes
Olá João,
No vídeo com a resolução do exercício é explicado a razão pela qual a opção D não é válida. Conseguimos ver no gráfico que o zero da segunda derivada é um número positivo, este tem que coincidir com o ponto de inflexão da função, no entanto, na opção D a abcissa do seu ponto de inflexão é um número negativo, logo essa opção não pode ser a resposta certa.
09 de Julho de 2019, 16h14
Mensagem de Ana Santos
Olá, boa tarde,
No exercício 16, a alínea 16.1 não está inteiramente resolvida. Sendo que, pede para determinar uma reta tangente para além da primeira derivada. Por acaso essa era exatamente a minha dúvida, como determinar a reta que é pedida.
Aguardo resposta, obrigada.
11 de Julho de 2019, 11h55
Mensagem de Vitor
Olá Ana,
Tens toda a razão, por lapso o vídeo apenas mostra o cálculo da primeira derivada, mas não mostra a reta tangente no ponto zero. Portanto, aqui vai o resto da resolução: `f´(0)=e^0(0^2+3xx0+1)=1xx(0+0+1)=1`.
Posto isto, já sabemos que o declive da reta tangente é `1`. Vamos agora calcular o ponto de interseção da reta tangente com a função: `f(0)=e^0(0^2+0)=0`. Assim sendo, o ponto de interseção é a origem do referencial, ou seja o ponto `(0,0)`. Como a tangente tem como equação `y=mx+b`, vamos agora substituir os valores de `x, y` e `m` para conseguir encontrar o `b`: `0=1xx0+b hArr b=0`. Fica determinada a reta tangente à função no ponto zero que é a seguinte: `y=x`. Espero que tenhas percebido.
16 de Maio de 2020, 23h07
Mensagem de Diana
Olá! Boa noite!
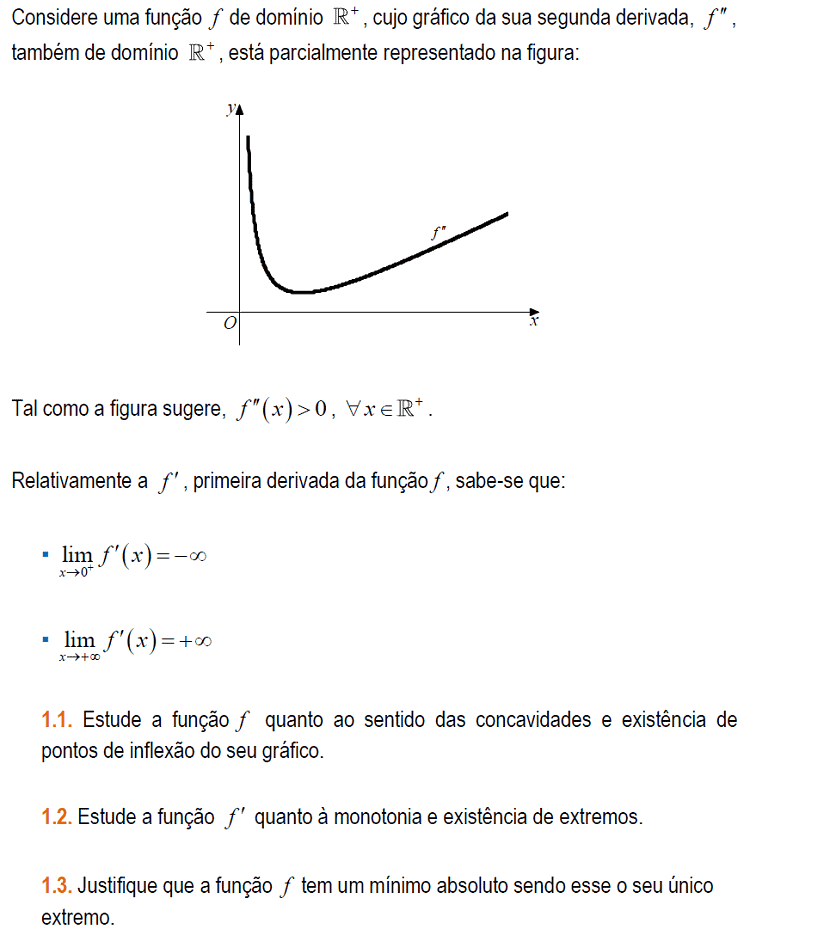
No exercício 19, no ponto 3 poderíamos responder à questão com o facto da segunda derivada ser uma função positiva em IR+? E consequentemente, que a concavidade da função f seria voltada para cima, sem pontos de inflexão, e com apenas um mínimo (que por isso, seria absoluto)?
Continuação de um bom trabalho!
17 de Maio de 2020, 09h53
Mensagem de Vitor Nunes
Olá Diana,
Aquilo que mencionas está certo, mas não é suficiente. Deves acrescentar que a primeira derivada possui um zero, uma vez que passa de sinal negativo para positivo. E que esse zero é um extremo da função, sendo um mínimo absoluto.
Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.
