Razões trigonométricas. (revisão)

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

Apesar de ser o polígono com menor número de lados, o triângulo é muito importante em processos de determinação de distâncias de difícil avaliação direta e na resolução de outro tipo de problemas.
A palavra trigonometria, de origem grega, pode ser decomposta em trígonos (triângulo) + metreo (medida), ou seja, significa medida de triângulos. Em qualquer triângulo tem-se três lados e três ângulos. O estudo da trigonometria permite estabelecer relações entre os lados e os ângulos dos triângulos.
Há referências a alguns aspetos relacionados com a ordem da trigonometria em vários domínios, de que se destaca a astronomia. Por exemplo no século V a.C., Hipócrates de Quios estudou relações entre arcos de circunferências e as respetivas cordas. Ao matemático e cosmógrafo alemão Johannes Muller Von Konigsberg, mais conhecido por Regiomontano, é atribuído o estudo da trigonometria, pela primeira vez, como uma ciência independente da astronomia.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
17 de Maio de 2020, 12h55
Mensagem de Diana
Olá! Bom dia!
Seria possível no exercício 4, ponto 2, concluir que a função d(x)= cos(x)+raizquadrada(8+cos^2(x))? Isto considerando que 9-sen^2(x) pode ser traduzido em 8+1-sen^2(x), e consequentemente 8+cos^2(x)?
Continuação de um bom trabalho!
18 de Maio de 2020, 09h52
Mensagem de Vitor Nunes
Olá Diana,
Como o exercício não pede para simplificar a expressão, não é necessário fazer isso. Em todo o caso, a simplificação que sugeres está absolutamente certa. É um passo inteligente concluir que `9-sin^2 x` pode ser escrito da forma `8 + cos^2 x`. Muito bem.
24 de Maio de 2020, 01h15
Mensagem de Rui
Olá,
Em relação a pergunta 4.2., eu fiquei sem entender a resposta, pois no intervalo pedido, os valores ultrapassam os 3cm que já sabemos serem máximos, sendo que PQ é a hipotenusa então OQ nunca pode ser maior do que três para o domínio pedido. No entanto, resolvendo a função d(0) que encontrámos dá 4. Porque é que isto acontece? Obrigado.
24 de Maio de 2020, 09h08
Mensagem de Vitor Nunes
Olá Rui,
Estás a interpretar mal o exercício. Volta a reler o enunciado e tenta perceber melhor como é que o ponto `P` se movimenta. Poderás verificar que a distância máxima de `d(x)` é alcançada quando o ponto `P` coincide com o ponto `A`. Nesse local o ângulo `x` tem zero graus de amplitude e `bar(OQ)=4`, porque resulta da soma de `bar(OA)+bar(AQ)=1+3`. Espero ter ajudado...

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.






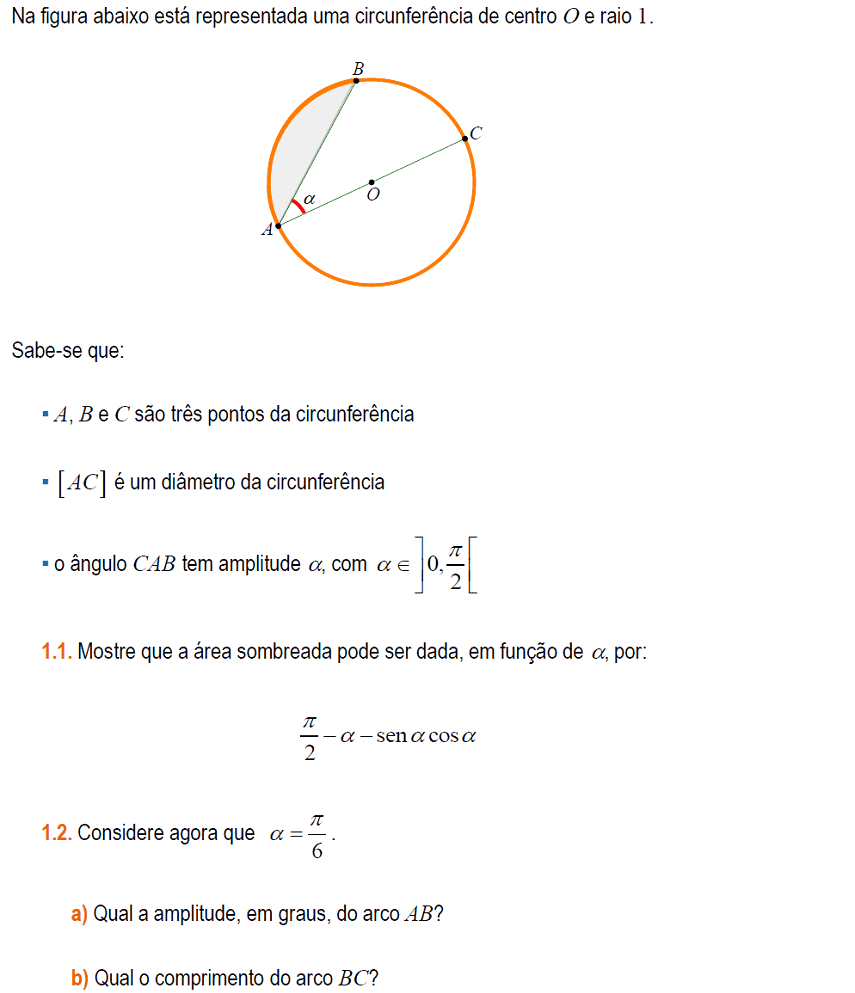

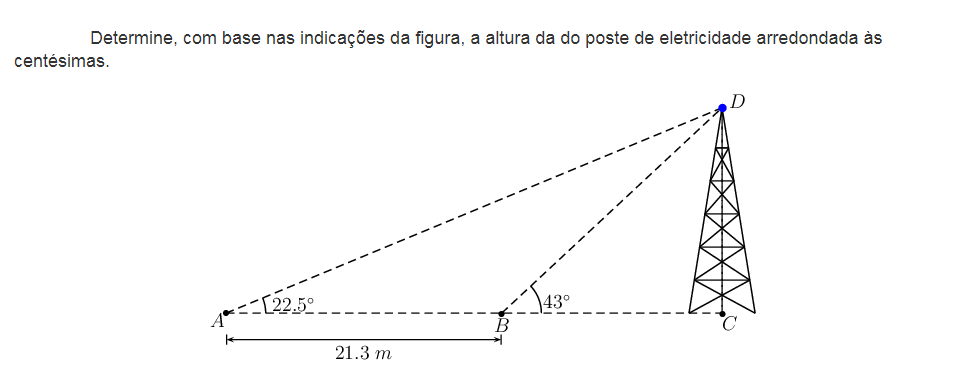
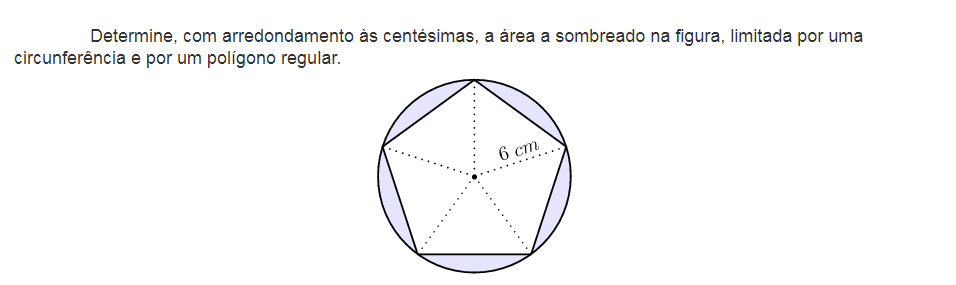
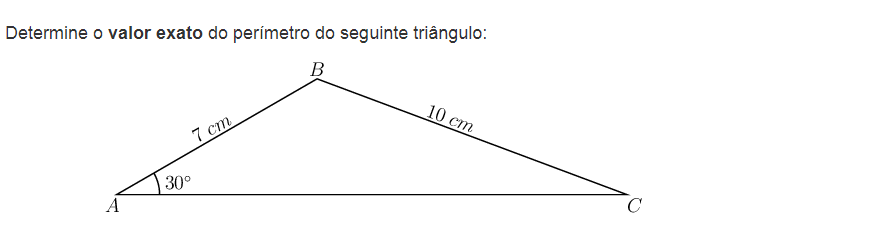



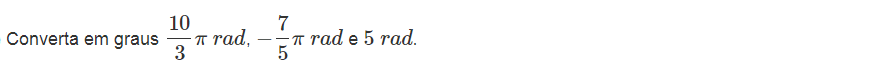
 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 