Sucessões limitadas. Determinar os minorantes e majorantes.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

Uma sucessão diz-se limitada quando o conjunto dos seus termos tem majorantes e minorantes, ou seja, quando é majorada e minorada.
O estudo da monotonia de uma sucessão poderá facilitar a classificação de uma sucessão em limitada e não limitada mas as situações são variadas e as sucessões podem não ser monótonas e ser limitadas, tal como podem ser monótonas e ser limitadas, tal como podem ser monótonas e não ser limitadas (por não serem majoradas ou minoradas). Muitas vezes, a escrita do termo geral numa outra forma, ou a representação gráfica são boas opções para investigar se a sucessão é ou não limitada.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
21 de Julho de 2016, 12h40
Mensagem de Bongo
Durante o cálculo não consigo determinar o minorante nem o majorante! Será que se escolhe aleatoriamente?
22 de Julho de 2016, 10h14
Mensagem de Vitor Nunes
Olá Bongo,
Normalmente não existe apenas um minorante e um majorante. Aquilo que existe é um conjunto de números que são designados por majorantes ou minorantes. Por exemplo, se uma sucessão for limitada é porque ela é minorada e majorada, ou seja, existe um conjunto de números, tais que, os termos dessa sucessão são sempre superiores ou inferiores respetivamente aos minorantes e majorantes. O processo de cálculo é feito por via analítica. Existem várias formas de calcular esses valores, sendo o mais comum a utilização de um processo conhecido como enquadramento.
27 de Fevereiro de 2017, 16h44
Mensagem de Tiago
Boas, tenho uma sucessão: un=(4n-3)/2. Sei que ela é crescente, logo o primeiro termo é minorante. Como descobrir o majorante? Eu penso que se divide o numerador pelo denominador, mas como o divisor não tem n... Pode-me ajudar sff.
28 de Fevereiro de 2017, 20h55
Mensagem de Vitor Nunes
Olá Tiago,
Normalmente só respondo a dúvidas que estejam relacionadas com exercícios presentes na página. No entanto, vou abrir uma exceção. De facto, a sucessão que indicas é monótona crescente. Logo é minorada e o primeiro termo faz parte do conjunto dos minorantes. Mas, como a sucessão não é limitada, ou seja, não é convergente mas sim divergente, à medida que o `n` tende para mais infinito o valor da sucessão também tende para mais infinito. E assim sendo, a sucessão não é majorada, logo não existem majorantes. Para demonstrar isso, basta calcular o limite da sucessão.
09 de Janeiro de 2018, 15h50
Mensagem de Inês Falcão
Olá, uma coisa que não percebo é: quando é que as sucessões não são limitadas?
Como é que sabemos se é limitada ou não?
Sei que apenas é limitada se tiver majorantes e minorantes! Mas tem sempre ou não? Obrigada.
11 de Janeiro de 2018, 09h33
Mensagem de Vitor Nunes
Olá Inês,
Um sucessão só é limitada se tiver majorantes e minorantes. Mas, nem todas as sucessões são majoradas ou minoradas. Por exemplo, na sucessão: `u_n = 2n`, experimenta substituir o `n` por números naturais, vais verificar que obtens números cada vez maiores. Assim sendo, esta sucessão, apesar de ter minorantes, não tem majorantes, logo não é limitada! Existem várias técnicas utilizadas para saber se uma sucessão é limitada ou não, uma das mais utilizadas consiste em tentar enquadrar a sucessão entre dois valores, se isso for possível, então é limitada.
05 de Junho de 2018, 20h49
Mensagem de Carla R.
Olá!
Sendo Un uma sucessão crescente, U1 é o minorante. Agora, fazendo o limite da sucessão esta não tende para infinito pelo que tem um majorante. Como o calculo analiticamente? Através da divisão do numerador pelo denominador ou há outra forma?
Aguardo resposta.
06 de Junho de 2018, 08h58
Mensagem de Vitor Nunes
Olá Carla,
Existem várias técnicas para isso. O cálculo do limite das sucessões implica por vezes levantar indeterminações e isso faz-se na maioria das vezes através dos chamados limites notáveis. No entanto, cada caso é um caso, não sendo possível explicar aqui todas as formas que existem para calcular o limite de uma sucessão.
03 de Março de 2019, 18h08
Mensagem de Cláudia
Boa tarde, no exercício 10 (b) (ii), era possível mostrar analiticamente que a sucessão é apenas majorada ou é só a minha falta de jeito?
04 de Março de 2019, 17h36
Mensagem de Vitor Nunes
Olá Cláudia,
Tendo em conta que a sucessão é uma restrição da função `f` ao conjunto `N`, e que esta última é uma função quadrática com a concavidade voltada para baixo, então a sucessão possui de certeza um conjunto de majorantes. Isto é mais ou menos óbvio, visto que a função possui um máximo absoluto. Para encontrar analiticamente esse ponto, basta encontrar o máximo da função. Para conseguir isso podemos calcular o seu vértice através da fórmula `V((-b)/(2a),(-Delta)/(4a))`.
08 de Abril de 2019, 18h41
Mensagem de Hadla
Olá, boa tarde! No exercício 8, não percebi porque dizemos que (-1/n) é menor OU IGUAL a zero. Não percebi este “igual”. Não seria sempre menor do que zero, assim como (+1/n) é sempre maior do que zero, e nunca igual?
Obrigada!!
08 de Abril de 2019, 20h46
Mensagem de Vitor Nunes
Olá Hadla,
Muito bem observado! Voltei a ver o vídeo com atenção e de facto existe uma pequena gralha, que felizmente não altera aquilo que queremos provar, que consiste em mostrar que a sucessão é limitada. Mas em todo o caso, tens toda a razão, deveria estar apenas menor que zero, em vez de estar menor ou igual a zero. As nossas desculpas e obrigado por ter reportar o erro!
08 de Maio de 2019, 16h59
Mensagem de Marta
No exercício que resolveu, eu obtive o minorante e o majorante de outra forma, tal que o majorante me deu 2 e o minorante 1. O minorante está certo?
08 de Maio de 2019, 17h03
Mensagem de Lúcia
Nunca tinha determinado o minorante como voçê determinou. Resolvi de outra forma e o valor do majorante coincidiu, mas o valor do minorante deu 0. Está certo?
09 de Maio de 2019, 10h12
Mensagem de Vitor Nunes
Olá Marta e Lúcia,
Primeiro convém esclarecer que uma sucessão limitada não possui apenas um minorante, mas sim um conjunto de minorantes. No exemplo do vídeo com a explicação da matéria é apresentada um sucessão, monótona crescente e limitada. Tendo em conta estes dois factos, uma vez que ela é crescente então o primeiro termo é um minorante. No caso desse exercício o valor do primeiro termo é `1//2`. Mas que fique claro, que todos os números inferiores a esse valor também são minorantes. Logo, `0` é um minorante válido, mas `1` já não é. Em relação ao conjunto dos majorantes aplica-se exatamente o mesmo conceito.
05 de Dezembro de 2019, 01h22
Mensagem de Alix
Olá,
No exercício 8, o menor número do conjunto dos majorantes de Un não deveria ser 1/2? Em vez de 1? Como n pertence sempre ao conjunto de números naturais, 1 nunca seria majorante. (Para o ser, n teria que pertencer ao conjunto de números inteiros, nesse caso n=-1 (U-1=1)).
Estou certo?
05 de Dezembro de 2019, 15h10
Mensagem de Vitor Nunes
Olá Alix,
Muito bem visto, tens toda a razão. Como referes, e bem, o primeiro termos da sucessão (`n=1`) vai ser `-1`, o segundo termo da sucessão (`n=2`) vai ser `1//2`, e assim por diante. Ora acontece que o segundo termo é o maior termo desta sucessão, logo o intervalo dos majorantes deveria começar neste termo. Apesar deste pequeno lapso, os exemplos dados estão corretos. O exercício pedia para determinar dois majorantes, sendo que os exemplos dados, `1` e `4` estão certos, uma vez que ambos os números fazem parte do conjunto dos majorantes. Obrigado por me ter chamado à atenção. Não deixes nunca de te questionar, porque assim vais longe.
23 de Fevereiro de 2020, 19h18
Mensagem de Joao Rodrigues
Boa noite, tenho estado a estudar com a minha filha, e temos uma dúvida num exercício, que pede para mostrar que é limitada a seguinte sucessão:
(-1)^n * (2/n)
Obrigado pela atenção.
24 de Fevereiro de 2020, 20h04
Mensagem de Vitor Nunes
Olá João,
Não tenho por hábito responder a dúvidas sobre exercícios colocados pelos utilizadores. Mas como estou com tempo, aqui vai: `(-1)^n` vai ser sempre igual a `1` ou a `-1`, dependendo do facto do expoente ser par ou ímpar, portanto isso só vai fazer variar o resultado da sucessão entre positivo e negativo. Quanto a `2/n` é limitado, porque numa fração, quanto maior o valor do denominador, mais perto o valor dessa fração está do zero. Logo a sucessão é limitada tanto inferiormente pelo primeiro termo, como superiormente pelo segundo termo.
14 de Abril de 2020, 16h29
Mensagem de Bia
Uma sucessão limitada tem sempre limite?
15 de Abril de 2020, 10h44
Mensagem de Vitor Nunes
Olá Bia,
Uma sucessão limitada terá que ter majorantes e minorantes. Isso não deve ser confundido com o cálculo de limite das sucessões, porque tratam-se de conceitos diferentes. No caso das sucessões limitadas, existe um número que é superior a todos os termos da sucessão, que se designa por majorante. De igual forma, existe um número que é inferior a todos os termos da sucessão, que se designa por minorante.
22 de Novembro de 2020, 14h40
Mensagem de Vizela Marques
Boa tarde. Tendo em conta que para saber se a sucessão é limitada teremos de estudar a monotonia da mesma, é possível mostrar que Un é limitada com uma sucessão monótona decrescente? É possível calcular o limite da sucessão quando o minorante é negativo? Obrigada.
23 de Novembro de 2020, 09h26
Mensagem de Vitor Nunes
Olá Vizela,
Uma sucessão pode não ser monótona e contudo ser limitada, por exemplo `U_n=(-1)^n`. Como pode ser monótona e ser também limitada, por exemplo `U_n=1/n-1`. Experimenta calcular a primeira meia dúzia de termos destas duas sucessões e irás verificar que ambas são limitadas. No caso da primeira sucessão, todos os termos estão entre `-1` e `1`. No caso da segunda sucessão, todos os termos estão entre `0` e `-1`. Logo, este último exemplo, responde às tuas duas perguntas. Visto que, temos uma sucessão com um minorante negativo, que é monótona decrescente e cujo limite é o número `-1`, porque a sucessão está cada vez mais perto desse valor, sem no entanto nunca o atingir.
19 de Janeiro de 2021, 18h28
Mensagem de Jéssica Azevedo
Boa tarde, eu tenho uma dúvida não é nenhuma dos exercícios aqui postos. Mas num outro exercício. Nesta sucessão (-1)^n (n+2) como eu faço para saber se é uma sucessão limitada ou não? Obrigada.
20 de Janeiro de 2021, 09h38
Mensagem de Vitor Nunes
Olá Jéssica,
Repara que `(-1)^n` é uma sucessão limitada, uma vez que à medida que o `n` representa um número par então vai ser `1`, se for um número ímpar vai ser o número `-1`. Mas, a sucessão `n+2` é monótona crescente, logo não é limitada. Como neste caso estamos a calcular o produto entre uma sucessão limitada e outra que não é limitada, o resultado vai ser uma sucessão que não é limitada.
19 de Outubro de 2022, 17h05
Mensagem de Hilário Mateus
A sucessão 1^n será limitada?
19 de Outubro de 2022, 17h41
Mensagem de Vitor Nunes
Olá Hilário,
Sim, essa sucessão é limitada. Repara que independentemente do valor do `n`, os termos da sucessão são sempre iguais a 1. Logo, a sucessão é limitada porque é majorada e minorada.

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.









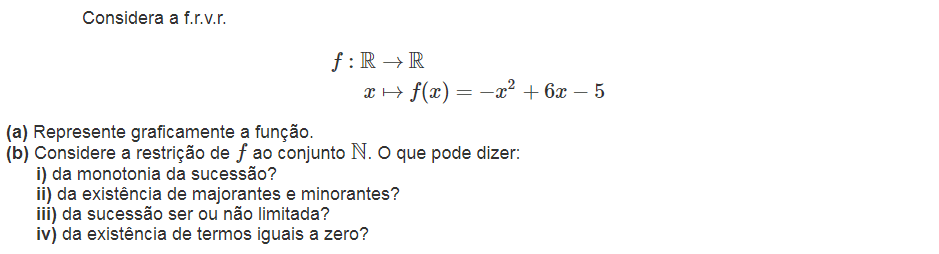
 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 