Poliedros e não poliedros.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

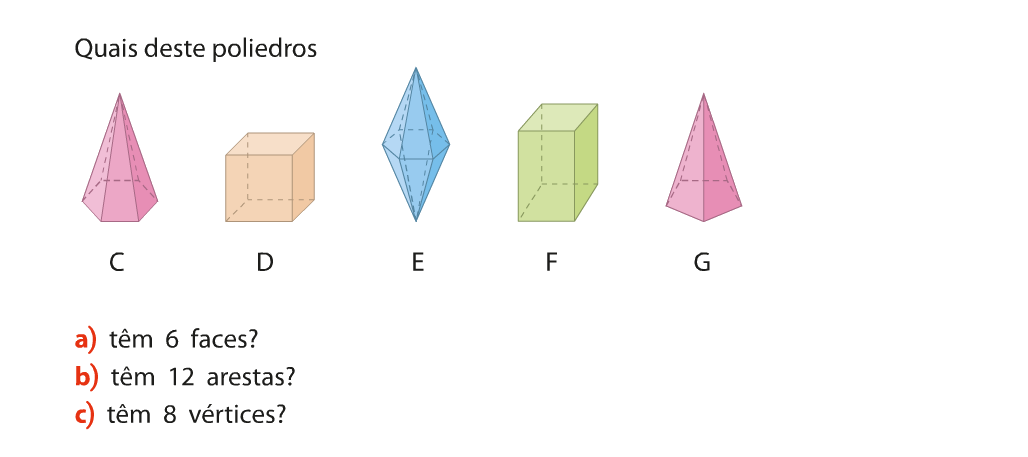
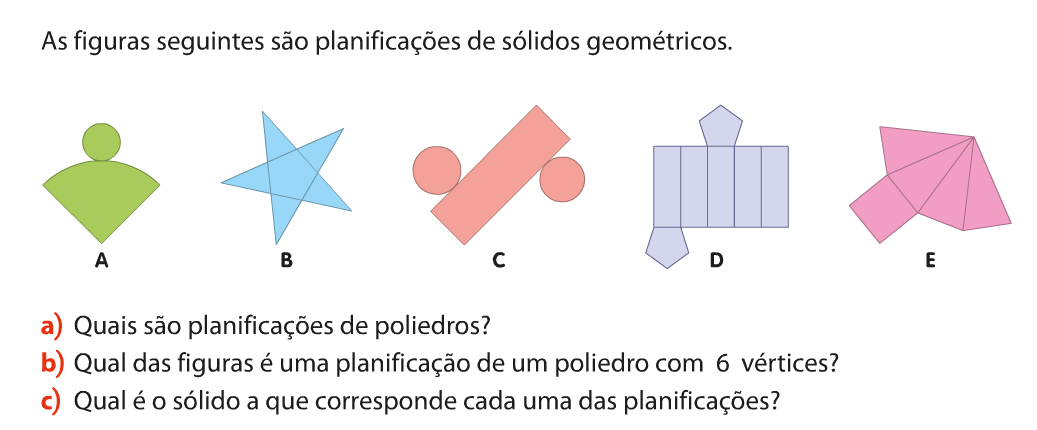
O Poliedro é um sólido geométrico que possui todas as faces planas. Enquanto que os Não-poliedros são sólidos que têm pelo menos uma superfície curva, como por exemplo: o cone, o cilindro e a esfera.
Todos os poliedros são constituídos por vértices, arestas e faces.
Os Poliedros regulares são sólidos cujas faces são polígonos regulares e geometricamente iguais. Foi Platão, sábio grego que viveu por volta dos 400 anos a.C., quem primeiro estudou os polígonos regulares e por esse motivo são designados sólidos de Platão.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
03 de Novembro de 2023, 18h57
Mensagem de Hélio Gonçalves Santos
Parabéns pelo trabalho. Usei este belíssimo trabalho para montar uma aula para minha sobrinha, que fará uma prova na próxima semana, e tinha dúvidas de como resolver possíveis questões à respeito.
Fico muito grato, e parabenizo-o pelo trabalho.
04 de Novembro de 2023, 12h54
Mensagem de Vitor Nunes
Olá Hélio,
Agradeço o comentário simpático.
Espero que a sua sobrinha consiga ter um bom resultado na prova.
28 de Novembro de 2023, 12h36
Mensagem de Francisca
Parabéns pelo belíssimo trabalho e principalmente por compartilhar.

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.


 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 