Função exponencial e função logarítmica.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

O estudo de funções, abordado até agora repartiu-se por duas vertentes:
- Generalidade sobre funções: definição, domínio, contradomínio, objetos, imagens, representação gráfica, zeros, injetividade, paridade, transformações dos gráficos por simetrias e/ou translações, inversão de funções injetivas, identificação das assímtotas, interpretação dos gráficos, …
- Estudo, em particular, de funções polinomiais, com destaque para o estudo das funções afins e quadráticas, funções racionais não polinomiais e funções irracionais, que no seu conjunto representam as funções algébricas.
Vamos agora dar inicio ao estudo de duas função não algébricas: a família das funções exponenciais e a das funções logarítmicas. Como é óbvio todas as aprendizagens relativas as “generalidades sobre funções” são indispensáveis para o estudo que se vai desenvolver. As funções exponencial e logarítmica desempenham um papel fundamental na modelação de problemas nas Matemáticas Aplicadas, na Economia, no Comércio e em muitas outras áreas. São usadas por exemplo nas Finanças para calcular o valor de um investimento, em Demografia para prever a dimensão de uma população, nas Ciências da Saúde para estudar a propagação de epidemias, na Arqueologia para datar achados pré-históricos, etc.
Explicação da matéria
Duração: 10:38
Duração: 10:31
Duração: 09:55
Duração: 11:06
Duração: 19:25
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
03 de Janeiro de 2015, 11h25
Mensagem de Samuel
Bom dia,
Não tenho dificuldade em utilizar as fórmulas dos logaritmos, mas ainda não consegui perceber para que é que servem os logaritmos, isso ajuda-nos em quê?
Já agora, parabéns pelo site, os exercícios de matemática fornecidos são muito úteis para podermos praticar e a resolução em vídeo vem mesmo ajudar quando estamos encalhados numa pergunta!
06 de Janeiro de 2015, 09h37
Mensagem de Vitor Nunes
Olá Samuel,
Dito de um forma simples, os logaritmos ajudam-nos a resolver equações em que a incógnita aparece como expoente de uma potência. Antes de teres aprendido esta noção de logaritmos não conseguias resolver este tipo de equações, agora já consegues!
Continua assim curioso, quando conseguimos entender o porquê das coisas, fica mais fácil aplicar esses conceitos, seja na matemática seja em qualquer área. Bons estudos!
05 de Março de 2015, 20h22
Mensagem de Maria Eduarda de Lima
Bom!! Eu queria saber se e possivel descrever funçoes logaritmicas com exemplo facil?!
06 de Março de 2015, 11h03
Mensagem de Vitor Nunes
Olá Maria Eduarda,
Não estou bem certo de ter entendido a pergunta.
A função Logarítmica é a função Inversa da função Exponencial. Como exemplo de uma função logarítmica temos `f(x) = log (x)` que é uma função crescente em todo o seu domínio, tal como a função exponencial. Mas, ao contrário desta, o seu crescimento vai sendo cada vez mais lento, à medida que o `x` caminha para mais infinito.
Se calhar, isto não foi de grande ajuda, mas a tua pergunta também não é clara.
11 de Março de 2015, 14h52
Mensagem de Tiago Ferreira
No exercício 11 eu atribuí um valor a k (por exemplo, 16, já que respeita a condição k>4) e fui resolvendo as equações até me dar o valor esperado. Posso fazer desta forma ou seria aconselhável resolver da forma proposta?
12 de Março de 2015, 09h38
Mensagem de Vitor Nunes
Olá Tiago,
Não está incorreto, mas a escolha do número 16 foi aleatória ou obedeceu a alguma regra? Digo isto, porque a soma da linha de um triângulo de Pascal é da forma `2^n` acontece que o 16 é `2^4` e portanto é um número válido, mas se tivesses escolhido o número 15, já não seria válido. No teu caso escolhendo o 16, permite-nos saber que o terceiro elemento da linha anterior é `text()^3C_2` e assim sendo, pode-se resolver as 4 hipóteses até dar este número. É uma boa estratégia, parabéns!
19 de Julho de 2016, 20h06
Mensagem de David Santos
Boas, no exercício 10, 2/3º passo, dependendo como virem as coisas, os parentesis estão errados. O k passa a ser o expoente de x. Não do logaritmo todo, nem da exponencial.
21 de Julho de 2016, 08h44
Mensagem de Vitor Nunes
Olá David,
Por vezes os professores também cometem erros, mas felizmente não é o caso. Voltei a ver o vídeo e a demonstração está correta. No 2º passo a variável `k` passa a ser o expoente de todo o logaritmo. Repara que o vídeo faz referência à seguinte regra das potências: `a^(nm) = (a^n)^m`. É a utilização desta regra que permite o uso dos parêntesis e assim concluir a demonstração. Espero que percebas a explicação.
03 de Janeiro de 2017, 15h41
Mensagem de Patrícia
Boa Tarde,
No exercício 13, eu não percebi porque é que o a elevado log a b é todo igual a 3, não deveria ser apenas o expoente (log a b)?
04 de Janeiro de 2017, 18h49
Mensagem de Vitor Nunes
Olá Patrícia,
Aconselho-te a voltar a ver o vídeo porque estás equivocada. Lá menciona que `a^(log_a b) = b` e não 3 como referes. Se calhar a minha letra não é das melhores e confundiste `b` com `3`.
22 de Novembro de 2017, 16h59
Mensagem de Joana
Boa tarde, como posso determinar o contradomínio de uma função logarítmica?
22 de Novembro de 2017, 18h44
Mensagem de Vitor Nunes
Olá Joana,
Normalmente não é feito o cálculo do contradomínio de uma função logarítmica porque este é `RR`. Já o domínio da função logarítmica, pode variar consoante a função. A forma mais fácil de obter o domínio consiste em garantir que o conteúdo do logaritmo é sempre maior que zero.
25 de Abril de 2021, 20h36
Mensagem de Juliana
Boa noite,
No exercício número 1, caso NÃO houvesse informação de que o "a é um número real maior que 1", haveria a necessidade de calcular o domínio, correto? Sendo verdadeira a afirmação anterior, sempre nos exercícios de logaritmo torna-se necessário o cálculo do domínio?
Obrigada desde já.
26 de Abril de 2021, 09h43
Mensagem de Vitor Nunes
Olá Juliana,
Normalmente neste tipo de exercício não é necessário calcular o domínio. isto porque, trata-se de uma expressão matemática que envolve logaritmos, em que nos é pedido para calcular o valor da expressão. Usualmente, o cálculo do domínio faz-se, quando estás a resolver uma equação e necessitas de saber se o resultado a que chegaste é válido, ou seja, se pertence ao domínio.

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.








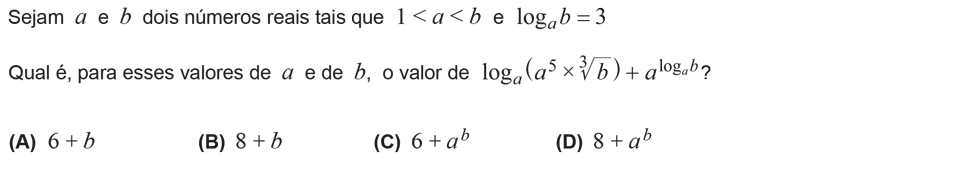




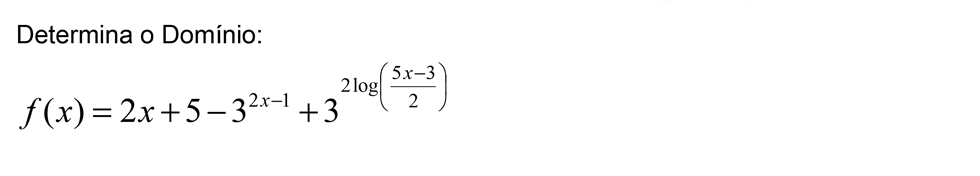

 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 