Derivadas de funções trigonométricas.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

Só a partir do séc. XVII, quando Descartes e Fermat introduziram as coordenadas cartesianas, se tornou possível transformar problemas geométricos em problemas algébricos. Com este avanço passou a ser possível estudar analiticamente funções, assim como, a sua aplicabilidade a outras ciências. Desde essa altura até ao presente, os cientistas, partindo de observações ou experiências realizadas, procuraram determinar uma fórmula ou função que relacione as variáveis em estudo. Foi enquanto se dedicava ao estudo de algumas destas funções que Fermat se deu conta das limitações do conceito clássico de reta tangente a uma curva. Foi a resolução dessa problemática, conhecida como o “Problema da Tangente”, que levou ao aparecimento do conceito de derivada.
Explicação da matéria
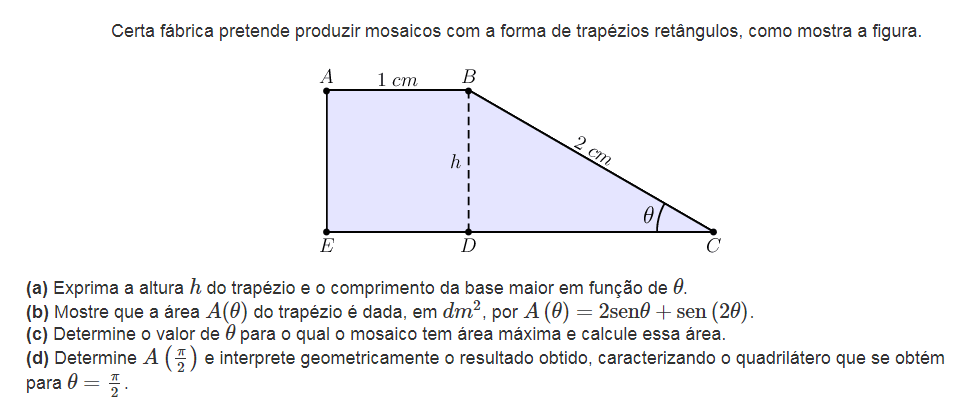
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
10 de Maio de 2021, 12h24
Mensagem de Juliana
Professor, bom dia.
No exercício nº 1, é explicado que "a derivada de uma constante é a própria constante", mas a derivada de uma constante, por definição, não é igual a zero?
Obrigada desde já.
10 de Maio de 2021, 12h28
Mensagem de Vitor Nunes
Olá Juliana,
Se calhar a frase não foi bem escolhida. De facto, a derivada de uma constante é zero, mas naquele exercício, o que se pretendia dizer, era que a derivada de uma constante que está a ser multiplicada por uma função é a própria constante. Fica feito o reparo.

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.











 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 