Dízimas finitas e infinitas.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

As frações cujo denominador é uma potência de base 10, por exemplo, 10, 100, 1000, etc. designam-se por frações decimais. Qualquer fração pode ser escrita na forma de fração decimal, desde que o seu denominador contenha apenas os fatores primos 2 e 5. Neste caso, essa fração corresponde a uma dízima finita.
Se numa fração, o denominador tiver pelo menos um fator primo diferente de 2 e de 5, então essa fração não pode ser equivalente a uma fração decimal, e corresponde a uma dízima infinita periódica.
Como curiosidade, fica a informação que todas as frações podem ser representadas por dízimas finitas ou por dízimas infinitas periódicas, mas nenhuma delas tem o período igual a 9. Por exemplo, o número `2,(9)` ou o número `4,3(9)` não pode ser representado em fração.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
06 de Outubro de 2024, 20h16
Mensagem de Rita
Como faço se houver uma dízima como: 1,2(3)
Existe outra forma diferente de resolver?
Já agora adorei o vídeo, ótima explicação!
07 de Outubro de 2024, 08h58
Mensagem de Vitor Nunes
Olá Rita,
Pode ser feito da mesma forma. Como o período da dízima só tem um algarismo, vamos multiplicar por 10. Vai ficar: `x=1,2(3) hArr 10x = 12,(3)`. Fazendo a subtração obtemos: `10x-x=12,333333-1,233333 hArr 9x=11,1 hArr x=(11,1)/9 hArr x=111/90 hArr x=37/30`.

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.
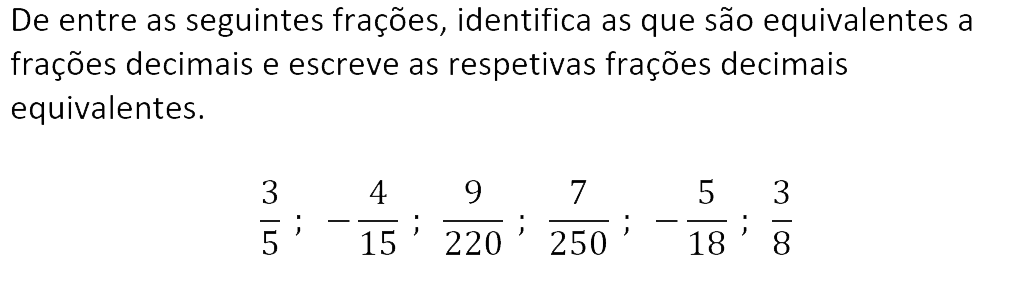


 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 