Equações com exponenciais e logaritmos.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

Atualmente, a utilização da calculadora e/ou computador permite resolver cálculos complicados de forma rápida e eficaz. A invenção dos logaritmos foi decisiva no desenvolvimento do cálculo do século XVI. Os logaritmos surgem como resposta as dificuldades dos matemáticos da época em lidar com cálculos complicados.
Quando em 1614, John Nepper publicou a “Descrição da Maravilhosa Regra dos Logaritmos”, pode dizer-se que se deu uma verdadeira revolução nos processos de cálculo. A ideia foi recebida com entusiasmo e imediatamente adotada e aperfeiçoada, pela simplificação que trazia aos complicados processos de efetuar multiplicações, divisões e potências, conhecidos e utilizados até então.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
04 de Agosto de 2016, 23h26
Mensagem de Rui Silva
Olá, a minha questão é a seguinte: no exercício n°9 alínea c), na parte em que 3^log x na base 3 + 2 passa para 3^log x na base 3 vezes 3^2. Como é que o ...+ 2 passa a ...vezes 3^2? Espero que percebam a minha dúvida e obrigado pela atenção.
PS: Este site está Excelente!!!
05 de Agosto de 2016, 11h39
Mensagem de Vitor Nunes
Olá Rui,
A resposta a essa pergunta é muito simples e está relacionada com uma propriedade das potências. Repara na seguinte expressão, um pouco mais simplificada do que a do exercício: `3^(x+2) = 3^x xx 3^2`. Isto é exatamente igual à questão que colocas (apesar deste exemplo não envolver logaritmos). Estamos aqui a aplicar uma regra das potências que nos diz que: "multiplicar duas potências com a mesma base é igual a manter a base e somar os expoentes". Espero que tenhas percebido a explicação!
12 de Novembro de 2016, 17h52
Mensagem de Ines
Boa tarde, no exercício número 7, porque é que a solução (C) não está correta?
Obrigado, é ótimo o trabalho que tem desenvolvido.
13 de Novembro de 2016, 08h50
Mensagem de Vitor Nunes
Olá Inês,
O vídeo com a resolução do exercício número 7 mostra passo a passo aquilo que temos que fazer para isolar a incógnita `x` e assim encontrar a solução correta. Não pode ser a solução (C) porque nessa solução nem sequer aparece o número real `a` que está presente no enunciado. Além do mais, um dos passos da resolução implica que o número `5` apareça como expoente da incógnita `y`. Na solução que referes isso não acontece!
07 de Fevereiro de 2017, 01h46
Mensagem de Cat
Boa noite professor.
Tem algum vídeo onde explica a mudança de variável em equações com exponenciais? Obrigado.
07 de Fevereiro de 2017, 08h00
Mensagem de Vitor Nunes
Olá Cat,
Todos os vídeos que temos estão disponíveis no site. Não me lembro, se foi gravado algum vídeo, com a explicação da mudança de variável em equações com exponenciais. Mas normalmente, essa mudança é feita quando se trata de uma equação exponencial do segundo grau, em que trocamos a variável `e^x` por `y`. Assim, dá-nos a possibilidade de utilizar a fórmula resolvente. Depois de termos as soluções da equação de segundo grau, voltamos a fazer a troca de variável, tendo o cuidado de garantir que a exponencial `e^x` nunca pode ser negativa. Lamento, não conseguir ajudar mais.
11 de Fevereiro de 2017, 01h06
Mensagem de Cat
Muito obrigada professor, ajudou imenso e com a resolução de exercícios consegui entender bem esta parte da matéria!

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.













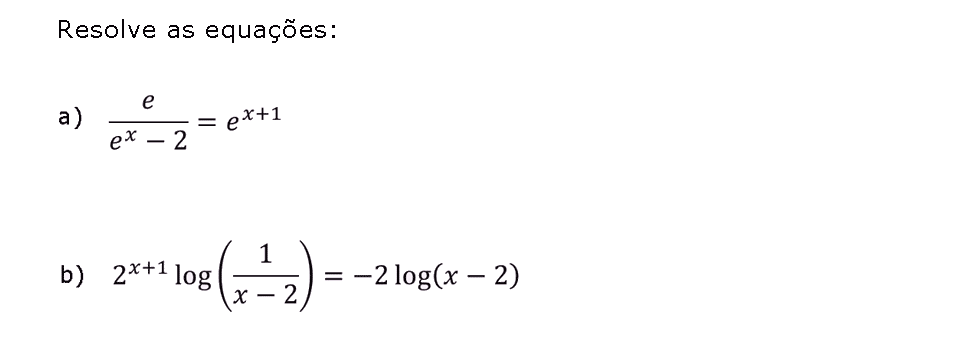





 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 