Inequações com exponenciais e logaritmos.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

O facto de a função logarítmica de base `a > 1` ser uma função crescente no seu domínio pode ser traduzida de forma simbólica para: `log_a x_1 < log_a x_2 hArr x_1 < x_2`. Esta definição permite resolver algumas inequações que envolvem logaritmos.
Atenção que se deve ter sempre em conta o Domínio de existência das expressões que figuram na condição tendo em consideração que só os números positivos tem logaritmo.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
16 de Abril de 2016, 15h44
Mensagem de Fábio
Boa tarde,
Fiquei com uma dúvida no exercício 2, se em (1 - x), o x < 1 logo a base do logaritmo é menor que 1. Porque é que quando passa o log para o outro membro para expoente não troca o sinal da inequação?
18 de Abril de 2016, 08h49
Mensagem de Vitor Nunes
Olá Fábio,
Tens razão quando afirmas que: se a base de um logaritmo for menor do que um, então ao aplicar a definição de logaritmo, o sinal de maior ou menor da inequação tem que ser invertido. Acontece que no exercício que referes, o número 2, a base do logaritmo não é `(1-x)`. A base é 3 e portanto é maior que um e assim não há lugar a troca de sinais quando se aplica a definição de logaritmo. Espero ter ajudado!
20 de Maio de 2019, 17h32
Mensagem de Beatriz
Boa tarde, professor.
Quais são os cuidados que devo ter, quando realizo exercícios que envolvam equações, inequações, ou mesmo limites com logaritmos, ao aplicar a propriedade log (a²) = 2 log (a) ?
Obrigada.
21 de Maio de 2019, 07h55
Mensagem de Vitor Nunes
Olá Beatriz,
Ao resolver equações e inequações que envolvam logaritmos devemos ter o cuidado de garantir que o número que está dentro do logaritmo não seja negativo. Isto está relacionado com o domínio da função logaritmo que, dada a sua definição, não permite o cálculo de logaritmos negativos. Na propriedade que referes não existe nenhum cuidado a ter, ela pode ser sempre aplicada, até porque `a^2` é sempre positivo.
29 de Maio de 2019, 05h03
Mensagem de Henrique
Olá! No vídeo do exercício 9_1.2 porque é que o Domínio é ]1,7]? Não será ]1,7[? Em suma, só queria tentar perceber se o Domínio da inequação do exercício está certo. Eu sei que não influencia na resposta final, mas queria perceber se me escapou alguma coisa ou foi só um pequeno lapso.
29 de Maio de 2019, 09h53
Mensagem de Vitor Nunes
Olá Henrique,
Estive a ver o vídeo com a resolução do exercício e tens toda a razão. Existe um pequeno erro no cálculo do domínio. Deveria ser `]1,7[` com ambos os intervalos abertos. Felizmente que isso não interfere com o resultado final, mas ainda assim fizeste bem em chamar à atenção.
08 de Maio de 2021, 11h27
Mensagem de Juliana
Bom dia, Professor.
No exercício nº 4, cheguei ao mesmo resultado, mas o resolvi de outra forma. Sendo assim, gostava de saber se está correto: transformei o número 1 do enunciado em log(x-3)≤log 10–log(x+2) ↔log(x-3)≤log10/(x+2)↔(x-3)≤10/(x+2)↔(x-3)(x+2)≤10. Dai em diante, está igual à resolução do vídeo. Meu raciocínio está correto?
Obrigada desde já.
08 de Maio de 2021, 11h50
Mensagem de Vitor Nunes
Olá Juliana,
Sim, podemos transformar o número `1` em `log 10`, e partindo desse pressuposto aplicamos as regras para a diferença de logaritmos. Está tudo muito bem.
08 de Maio de 2021, 12h27
Mensagem de Juliana
Bom dia, Professor.
No exercício nº 6, na representação do quadro de sinais, foi desenhada 2 colunas para que os valores dos zeros fossem preenchidos, ou seja o zero de x+23/4 e o zero de 2^-x. Porém, não há zero para 2^-x, pois a função nunca tocará o eixo do x, pois quando x tende para o infinito, o y tende para zero, mas nunca chegará a ser zero. Sendo assim, a representação do quadro de sinais, necessita de 1 coluna apenas para o zero de x+23/4, correto?
Obrigada desde já.
08 de Maio de 2021, 16h16
Mensagem de Vitor
Olá Juliana,
Sim, aquele quadro de sinais que está no vídeo é apenas uma exemplificação. Neste caso, como a função exponencial `2^-x` não tem zeros e é sempre positiva, nem sequer precisamos de fazer o quadro de sinal.

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.






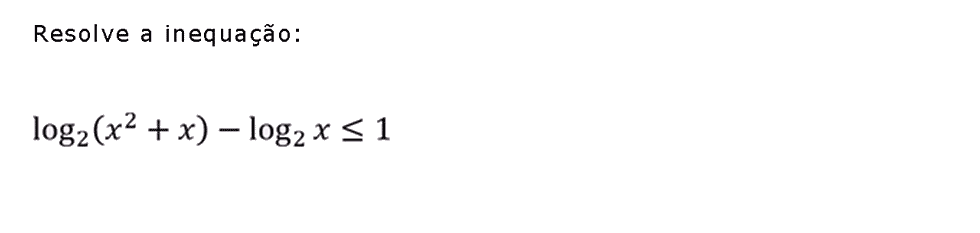




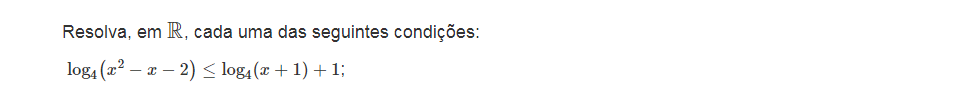
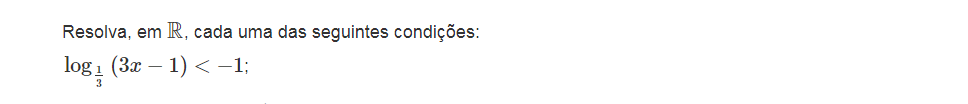
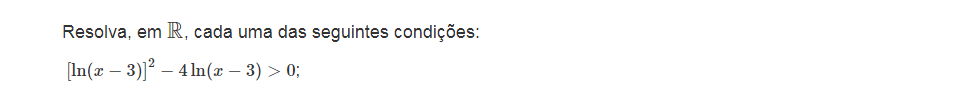
 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 