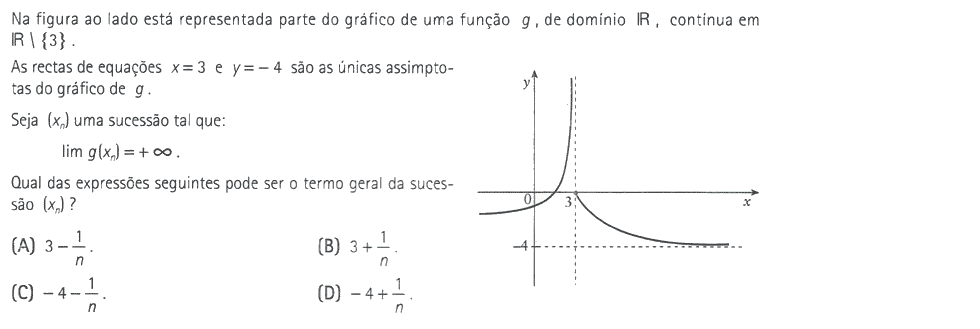
Limites de sucessões. Limite segundo Heine.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

A formalização do conceito de limite é feita recorrendo às sucessões de números reais:
Dada uma função `f`, diz-se que `f(x)` tende para `b` quando `x` tende para `a`, e escreve-se `lim_(x->a) f(x)=b`, se a toda a sucessão `(X_n)` de valores de `x` que tende para `a` por valores do domínio diferentes de `a`, corresponde uma sucessão `f(X_n)` de valores de `f(x)` que tende para `b`.
A definição anterior é devida ao matemático alemão Heinrich Eduard Heine e é conhecida precisamente como definição de limite segundo Heine.
Explicação da matéria
Duração: 17:40
Duração: 12:56
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
09 de Julho de 2016, 06h32
Mensagem de Euclides
O que são limites?
12 de Julho de 2016, 08h31
Mensagem de Vitor Nunes
Olá Euclides,
Tens um nome muito interessante, relacionado com uma grande personalidade matemática!
Falamos em limites quando queremos descobrir para qual valor uma sucessão ou uma função tende à medida que o seu termo ou objeto se aproxima de um determinado valor. Os limites são usados no cálculo diferencial e em outros ramos da análise matemática para definir derivadas e estudar a continuidade de funções.
23 de Janeiro de 2017, 22h35
Mensagem de Rafael
Um enorme obrigado pelas suas aulas professor. É das poucas matérias em que tenho dificuldades, mas assim ajuda muito!
24 de Janeiro de 2017, 08h20
Mensagem de Vitor Nunes
Olá Rafael,
É muito gratificante para nós quando vemos o nosso trabalho ser reconhecido. E o maior reconhecimento que podemos obter dos nossos alunos é ver que eles estão a aprender e além disso sentir que estão a gostar do que estão a aprender. Continua assim, tenho a certeza que vais obter excelentes resultados!
21 de Fevereiro de 2017, 11h59
Mensagem de Cat
Bom dia professor. Tenho uma dúvida em relação aos valores à direita e à esquerda de um dado número, quando aplicados em limites. Por exemplo, no caso de se querer o valor de lim g(x) quando x->2-, após substituir o valor na função se der uma fração do tipo 3/0, o 0 é um 0+ ou um 0-? E o valor do lim será +oo ou -oo?
Tenho dúvidas em relação a esses valores e já por algumas vezes que o resultado me deu mal, devido a não saber se o valor é + ou - :/ Obrigada.
22 de Fevereiro de 2017, 08h56
Mensagem de Vitor Nunes
Olá Cat,
Podes utilizar a seguinte estratégia: se por exemplo estiveres a calcular um exercício em que `x->2^+` então substitui o `x` por `2,1` e verifica se o resultado dá positivo, nesse caso trata-se de `0^+`, caso contrario é um `0^-`. Se `x->2^-` então substitui o `x` por `1,9` e faz a mesma verificação anterior. Depois de saber se é um zero mais ou um zero menos, basta aplicar a regra dos sinais na divisão, para decidir se o valor da fração é um mais infinito ou um menos infinito. Boa sorte para os testes!
23 de Novembro de 2017, 14h20
Mensagem de Inês
Boa tarde, porque é que quando o limite de alguma coisa dá um número sobre zero ( sem sinal ) não existe ?
Nestes casos devo calcular os limites laterais para comprovar que são diferentes e logo o limite não existe ?
24 de Novembro de 2017, 12h03
Mensagem de Vitor Nunes
Olá Inês,
Primeiro esclarecimento: não é verdade que o limite não existe quando temos um número sobre zero. O problema deste caso é que quando o denominador tende para zero, o valor da fração tende para infinito, mas não sabemos se é mais infinito ou menos infinito! Para descobrir isso, precisamos de verificar, se o zero do denominador é um zero mais ou um zero menos. E é aqui que entram os limites laterais, se forem iguais o limite existe, se forem diferentes não existe!
09 de Janeiro de 2019, 17h59
Mensagem de Ben
Gostei de matéria. Consegui entender um pouco mais sobre limites. Isso já é um bom sinal!
09 de Janeiro de 2019, 18h23
Mensagem de Vitor Nunes
Olá Ben,
Ainda bem, fico contente por saber. O meu conselho a todos os alunos é que resolvam o maior número de exercícios possível. Quanto mais praticarem, mais fácil tudo se vai tornando. Tentem resolver os exercícios sozinhos antes de ver a resolução em vídeo. Depois de ver o vídeo tudo parece muito fácil porque estamos a seguir o raciocínio de outra pessoa. O mais difícil muitas vezes é chegarmos lá sozinhos. Por isso força e bom trabalho!
06 de Maio de 2019, 16h52
Mensagem de Hadla
Olá, boa tarde! Fiquei confusa com o exercício resolvido que mostra que lim f(un) é diferente de f(lim un). Eu percebo que os dois são diferentes, mas achei que o limite não existiria (refiro-me ao exercício do sumário: exemplos práticos em que se tem a função descontinua em e). Penso que minha confusão seja pelo fato de f(e) ser diferente dos limites laterais quando un->e (os limites tendem a 1 e o f(e)=-1. Definições diferentes de limite nos dão limites diferentes? Muito obrigada!
07 de Maio de 2019, 08h38
Mensagem de Vitor Nunes
Olá Hadla,
Aquilo que o vídeo explica é que, por vezes, o `lim f(u_n) != f(lim u_n)`, isto acontece quando a função é descontinua no ponto para onde tende a sucessão! Mas o vídeo explica claramente que o limite existe sempre, e que para determinar o seu valor não deve ser utilizada a igualdade referida anteriormente, porque pode levar a que o aluno cometa enganos, uma vez que nem sempre ela é verdadeira.
15 de Dezembro de 2019, 20h07
Mensagem de Tomás
Olá professor,
Sou um aluno externo, e não tenho nenhum professor a quem perguntar isto, sei até que é uma pergunta um pouco "estúpida", mas o professor tem conhecimento se no exame, os exercícios de limites tanto de funções como sucessões, usam "técnicas" mais fáceis ou difíceis? É que por vezes encontro exercícios que tem explicações tão complexas que mesmo depois de ver não percebo a 100% o que se passou. Estes que o professor aqui põe são perceptíveis, mas alguns fico mesmo "à toa". Obrigado pelas aulas.
15 de Dezembro de 2019, 21h49
Mensagem de Tomás
Vou postar aqui 2 exemplos de que falo, se o professor me puder ajudar a perceber a solução ficaria agradecido!
Calcule lim(√16n^2+2n -4) a raiz apenas cobre o 16n^2+2n
Calcule lim(3n^2+4/3n^2)^2-n^2
Se pudesse explicar como funciona a resolução de ambos, o melhor que conseguir, a partir dos meios disponíveis seria excelente! Se não lhe der jeito nenhum não há problema, fico agradecido na mesma, as aulas ajudam muito!
16 de Dezembro de 2019, 09h09
Mensagem de Vitor Nunes
Olá Tomás.
Não tenho por hábito resolver exercícios propostos pelos alunos, mas como vejo que estás um pouco perdido, vou abrir uma exceção. Esta é a resolução do primeiro exercício:
`lim(sqrt(16n^2+2n)-4)` `= sqrt(lim(16n^2+2n))-lim 4)` `= sqrt(lim(16n^2))-4 ` `= sqrt(+oo)-4` `=+oo`
Quanto ao segundo exercício, não vou resolver aqui, mas tenta seguir os seguintes passos: 1) colocar tudo com o mesmo denominador; 2) simplificar o conteúdo do primeiro parêntesis; 3) aplicar o caso notável da Diferença de Quadrados; 4) escolher o termo de maior grau; 5) substituir o `n` por mais infinito.
Em relação à tua primeira pergunta, no exame costumam surgir cálculos de limites complexos, sendo que, muitos deles envolvem levantar indeterminações. Esta matéria só se aprende praticando, por isso, tenta resolver o máximo de exercicios sobre este tema que conseguires. Boa sorte.
27 de Outubro de 2020, 14h57
Mensagem de Ana
No limite de uma sucessão, no estudo de uma indeterminação, quando contém raiz que indeterminação uso?
27 de Outubro de 2020, 17h50
Mensagem de Vitor Nunes
Olá Ana,
Isso vai depender do tipo de indeterminação. A técnica a utilizar não está dependente da existência de uma raiz, mas sim se estamos na presença de uma indeterminação do tipo zero sobre zero, infinito sobre infinito, zero vezes infinito ou infinito menos infinito. Para cada um destes quatro tipos de indeterminação, existe uma técnica diferente que deverás conhecer e saber utilizar.
02 de Junho de 2021, 17h02
Mensagem de Ana
No exercício 4 no último exercício chega a um ponto em que tem algo a dividir por -1. E quando aplica o limite esse -1 desaparece porquê?
02 de Junho de 2021, 19h03
Mensagem de Vitor Nunes
Olá Ana,
De facto tratou-se de um esquecimento. Mas, se vires o vídeo até ao fim, irás reparar que na parte final da resolução desse exercício, o erro é detetado e corrigido. Em todo o caso, obrigado pelo comentário, significa que estás a prestar atenção!
02 de Fevereiro de 2022, 15h13
Mensagem de Sam
A aula é muito explicativa, mas poderia me ajudar? Tenho dificuldade em limites, poderia me informar por onde devo começar para perceber bem?
02 de Fevereiro de 2022, 18h18
Mensagem de Vitor Nunes
Olá Sam,
A minha sugestão é começar por ver as aulas com atenção para poder perceber bem a matéria. O próximo passo consiste em tentar resolver cada um dos exercícios que propomos. Só praticando é que conseguimos interiorizar os conhecimentos adquiridos. Assim que dominares os conceitos relativos a esta aula, avança para a próxima. Boa sorte!
13 de Junho de 2024, 02h37
Mensagem de Eliandro Mambo
Tenho uma duvida professor, se multiplicar 0 x 0 fico com quanto? É uma indeterminação?
13 de Junho de 2024, 14h29
Mensagem de Vitor Nunes
Olá Eliandro,
A multiplicação `0 xx 0` não é uma indeterminação. O resultado deste produto é zero.
Só existem 4 tipos de indeterminação, que deverás saber levantar: `00 - 00`, `0 xx 00`, `00 / 00`, `0/0`

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.



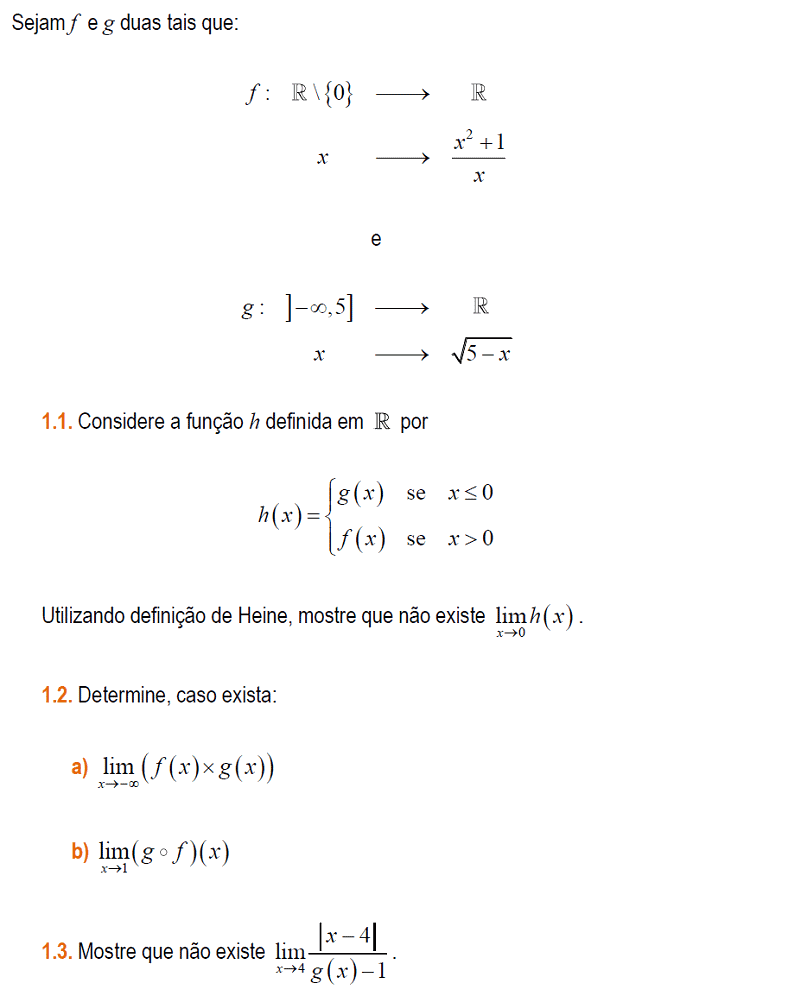





 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 