Lugares geométricos do plano.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

A aceitação plena dos números complexos só teve lugar no século XIX com os trabalhos de Gauss e Hamilton que permitiram que todos os matemáticos reconhecessem as potencialidades oferecidas pelos números complexos. Combinando a ideia de comprimento com a de direção e sentido num só número, os complexos alcançam um gigantesco campo de aplicações. A Física e a Eletricidade, por exemplo, não dispensam atualmente os cálculos com números complexos.
Também no âmbito da geometria, vamos ver que é possível caracterizar facilmente alguns lugares geométricos do plano (conjunto de pontos que satisfazem uma ou mais condições) por meio de condições com variável complexa. A interpretação do módulo de um número complexo como a distância da sua imagem geométrica à origem do referencial (ou como forma da sua representação vetorial) e o conceito de argumento de número complexo como inclinação da sua representação vetorial, permitem definir, desde já, alguns lugares geométricos.
ATENÇÃO
Nos novos programas de Matemática A, a forma de representar um número complexo na forma trigonométrica sofreu alterações. Já não se utiliza a notação: `z = rho.cis(theta)`.Em todas as aulas ou exercícios onde aparecer esta notação, ela deverá ser entendida como sendo: `z = |z| e^(i theta)`. Em todo o caso, o seu significado não se altera, continua a ser: `z = |z| (cos theta + i sin theta).`
Explicação da matéria
Exercícios resolvidos
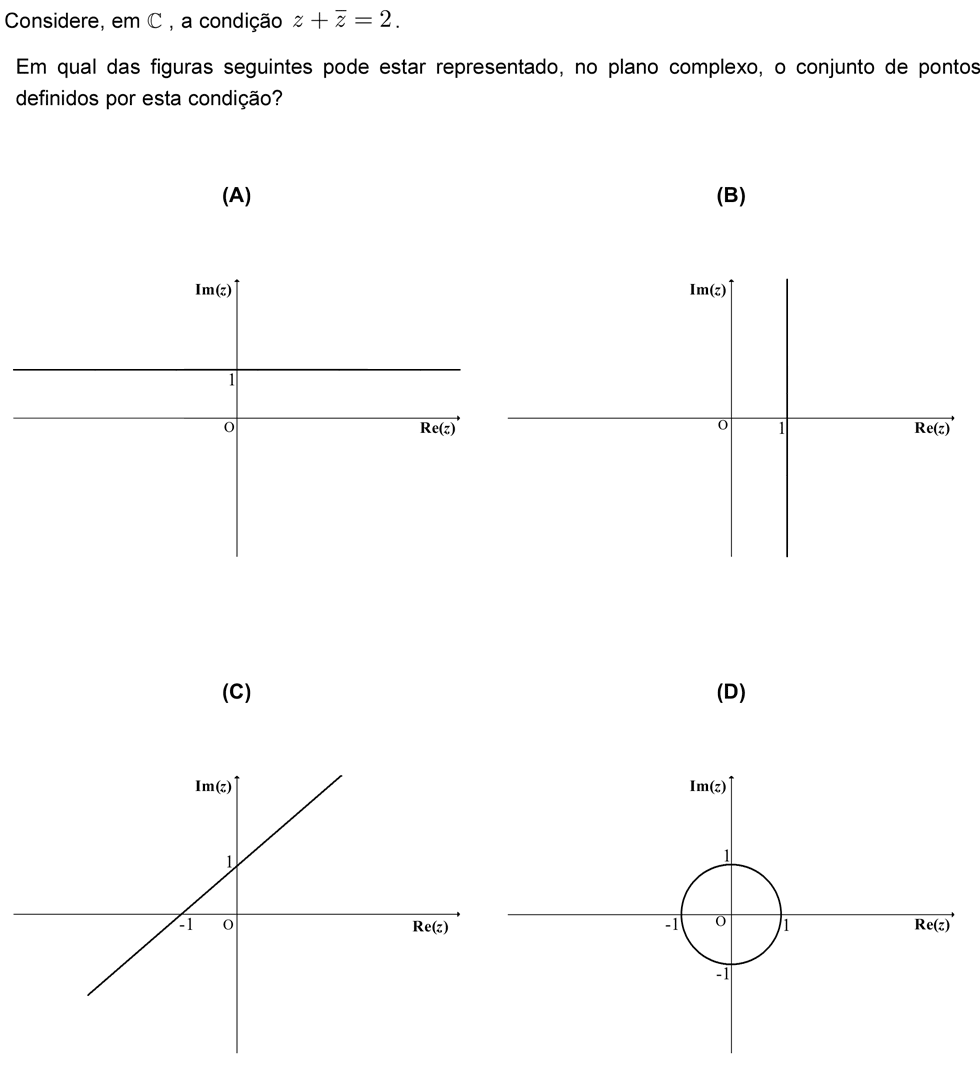
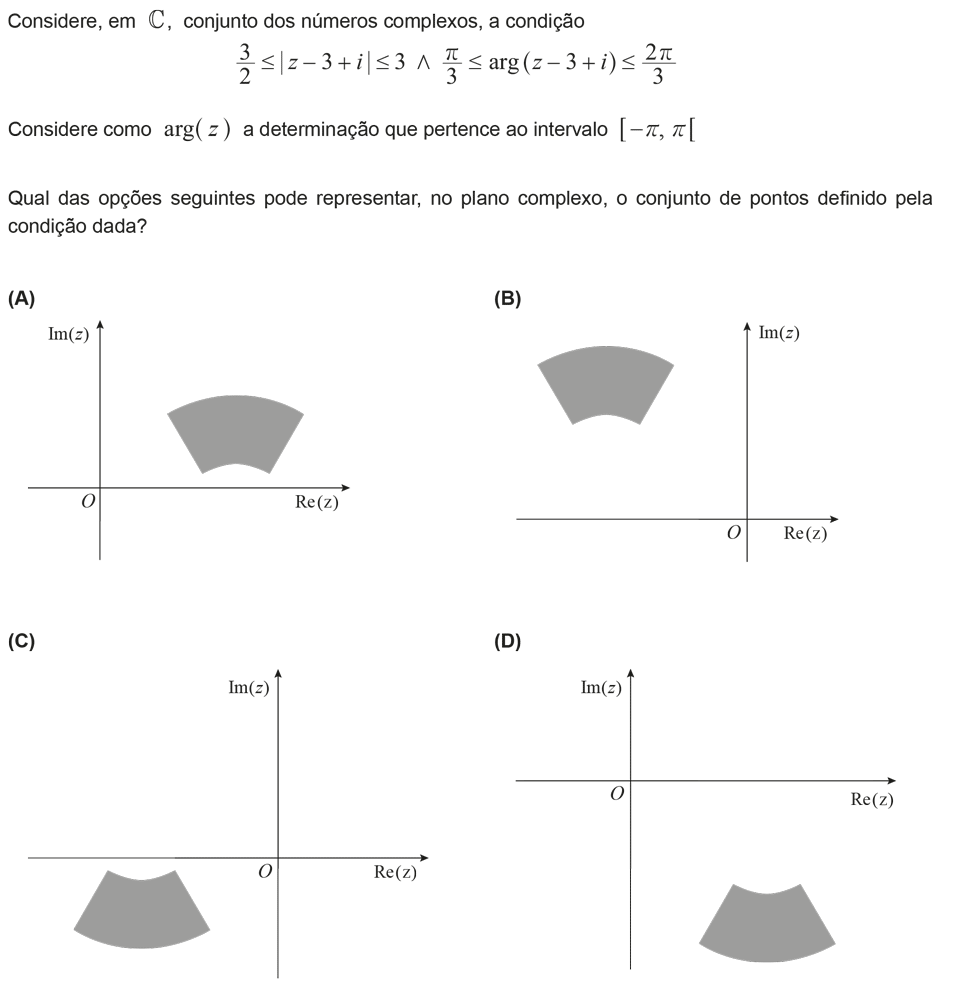
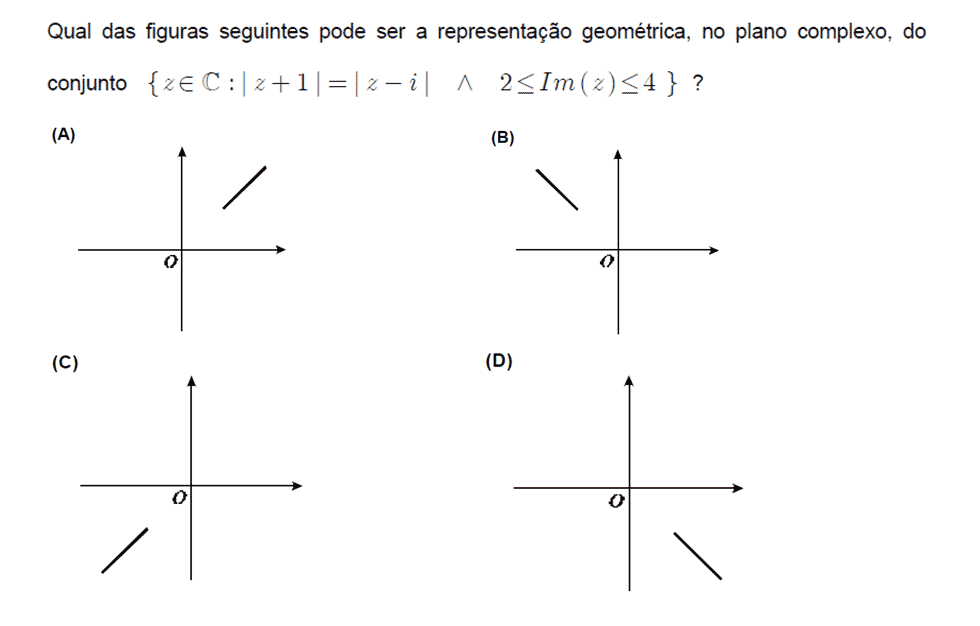
Nível:
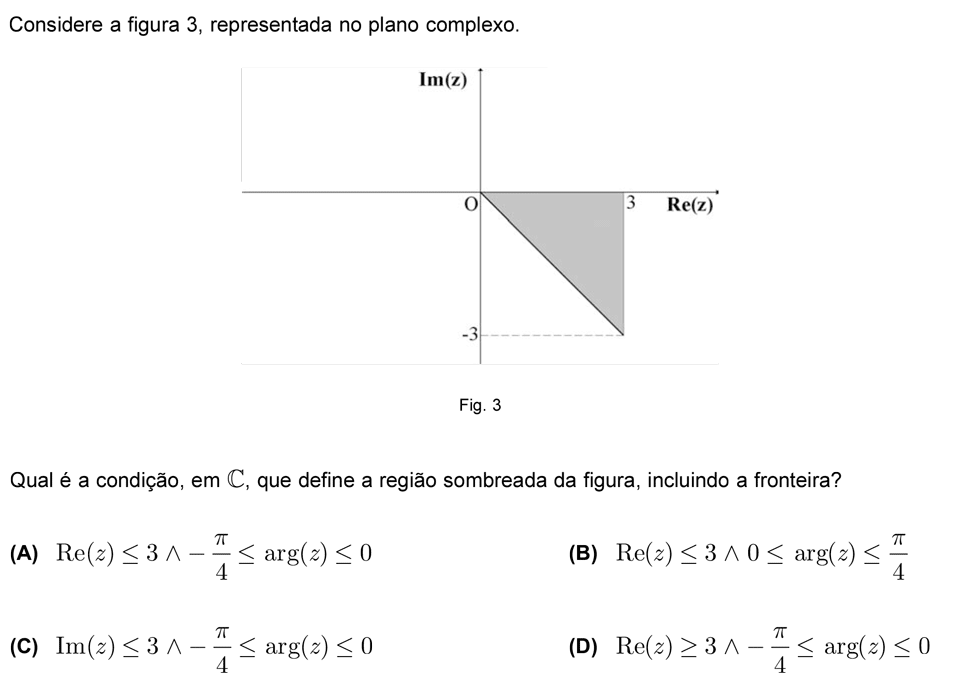
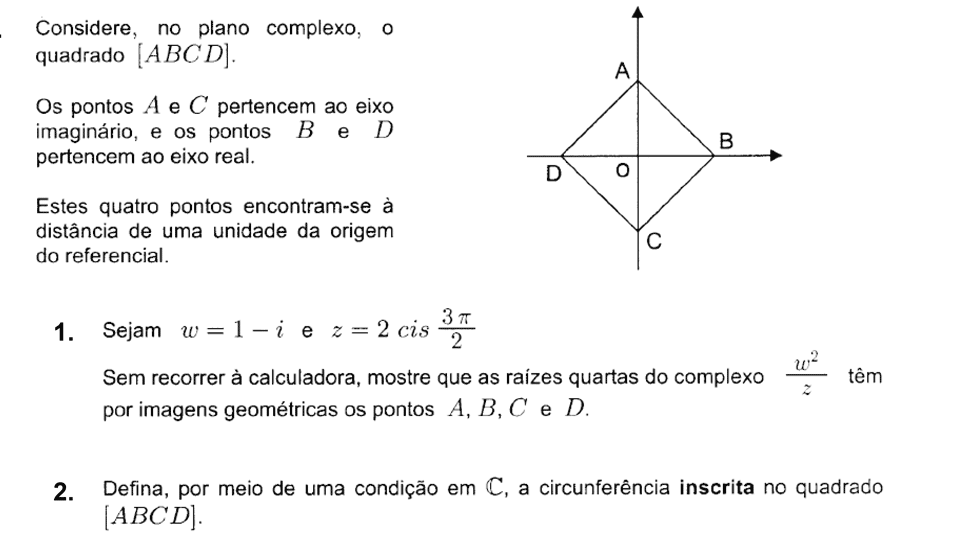
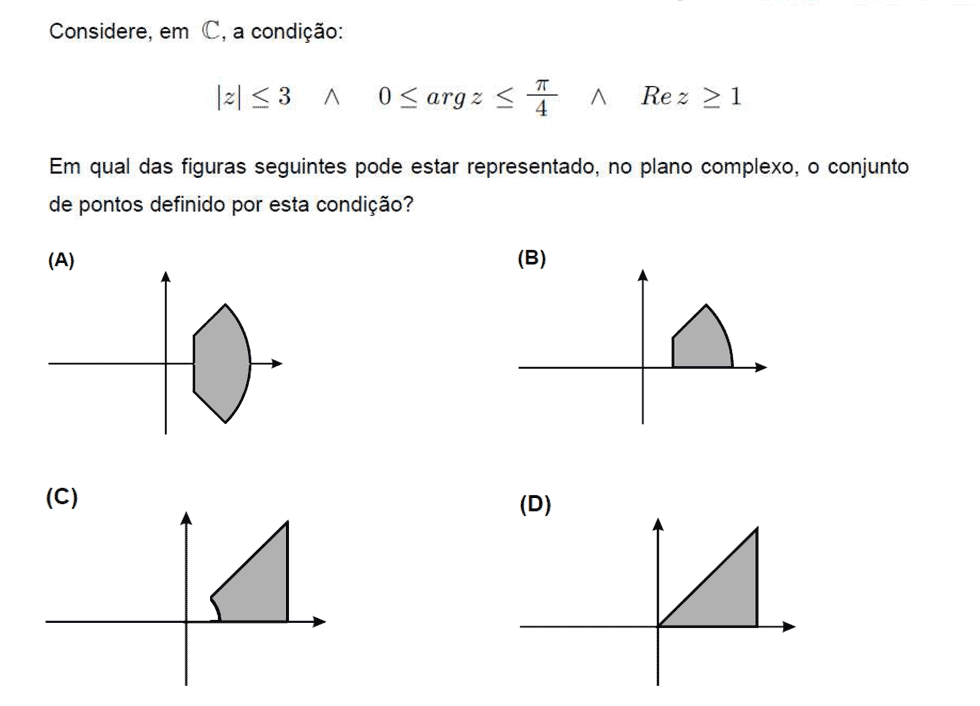
Nível:
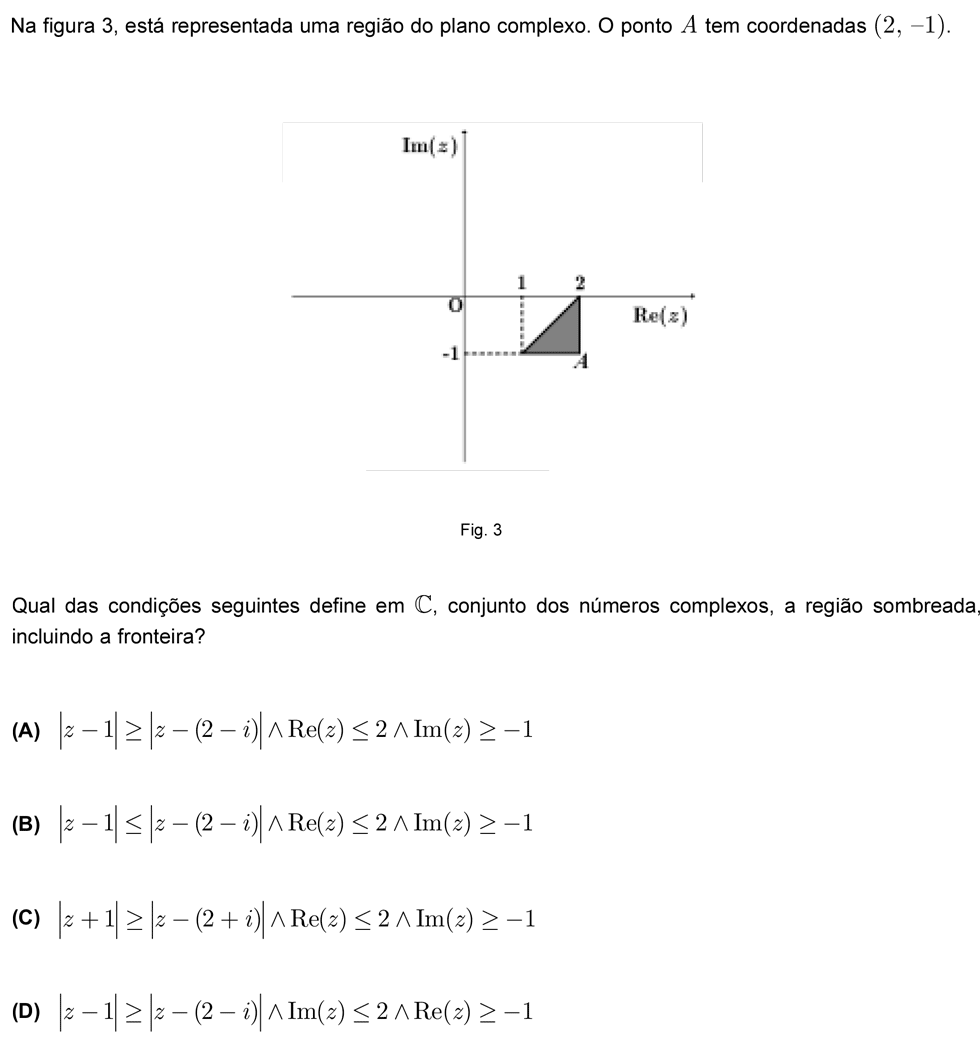
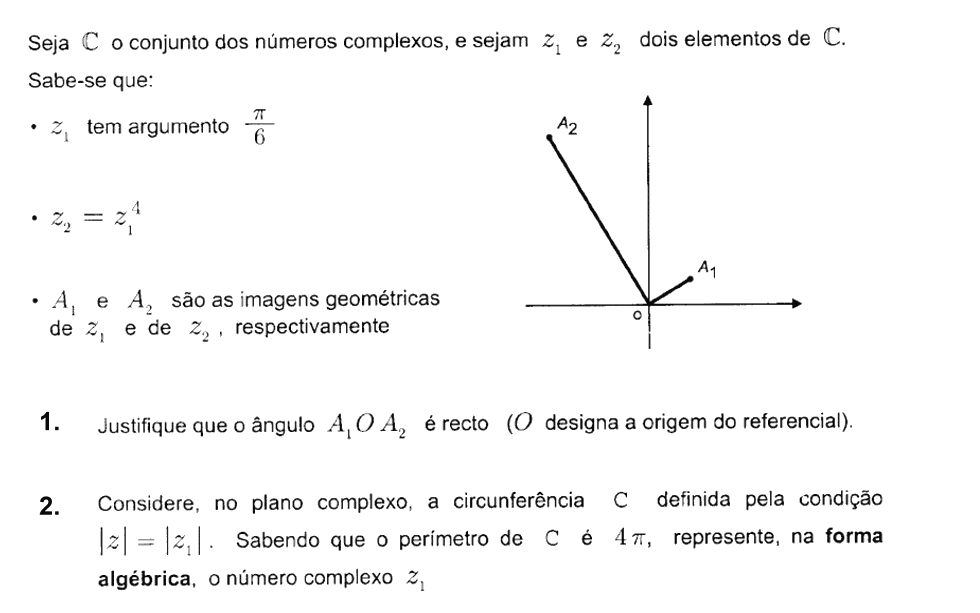
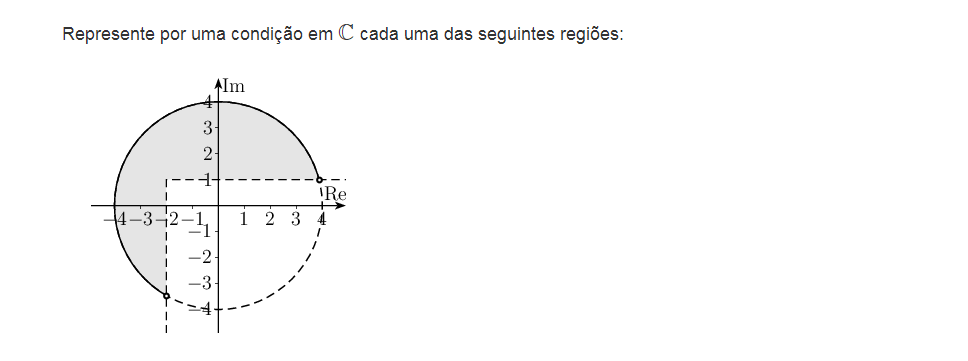
Nível:
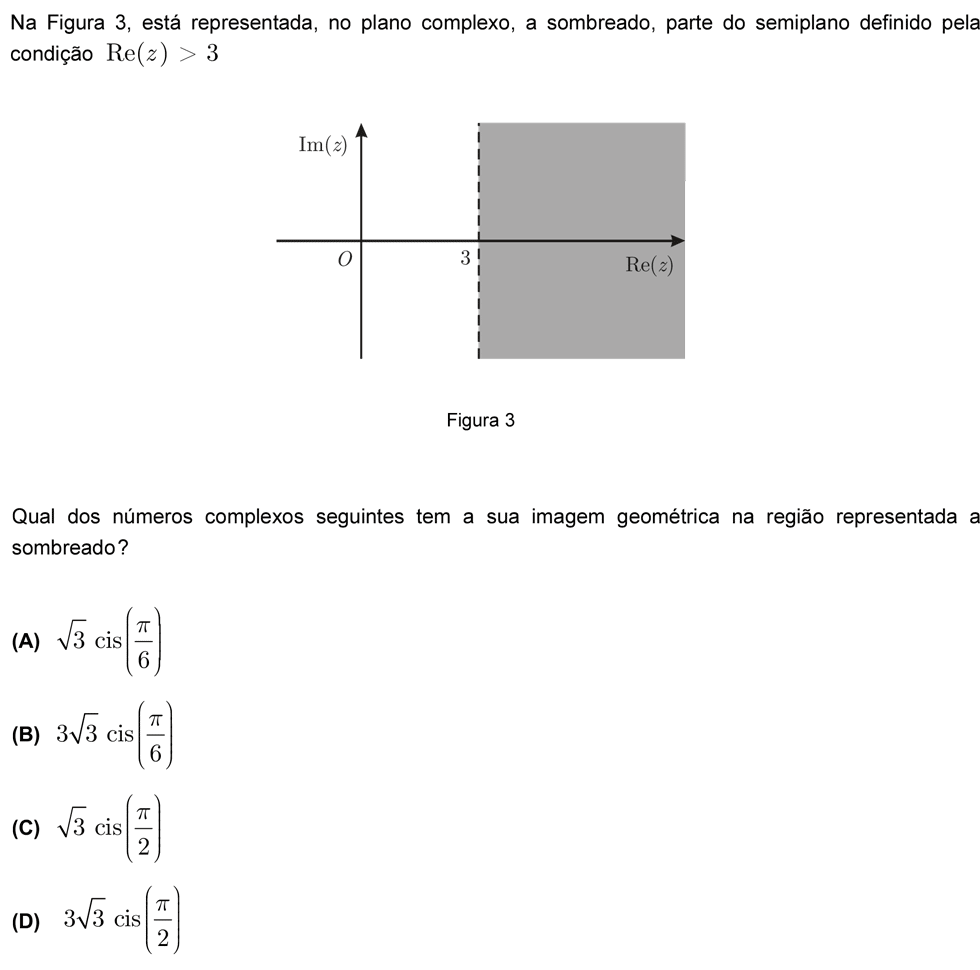
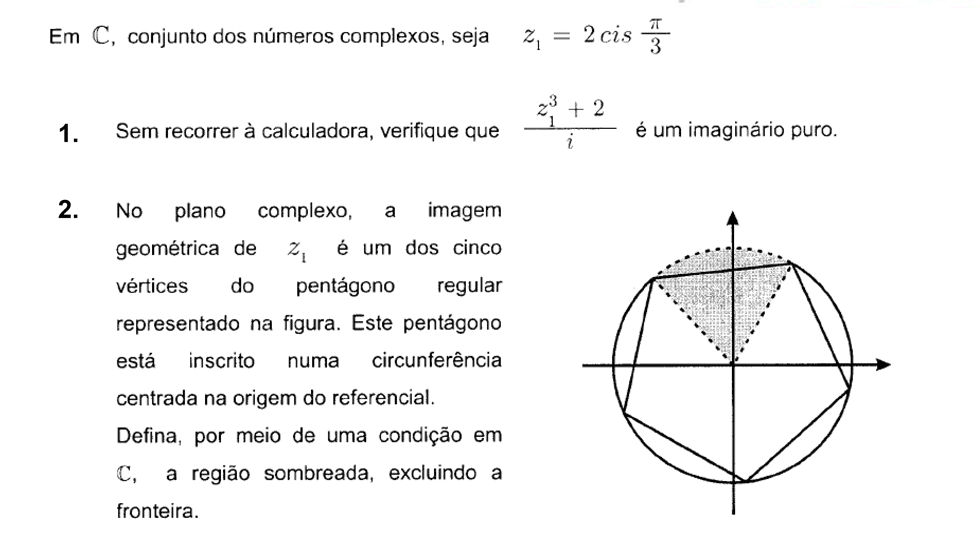
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
07 de Junho de 2016, 15h42
Mensagem de Catarina
Boa Tarde!
Não percebo porque é que a (C) do exercício 11 não pode ser. Segundo o que explicou no video é um ponto, eu resolvi, mas dá igual a 0. O que é que isso significa? Obrigada pela atenção.
08 de Junho de 2016, 23h38
Mensagem de Vitor Nunes
Olá Catarina,
Na resposta (C) do exercício 11 temos `3z+2i=0`, se resolvermos esta equação em ordem a `z` obtemos: `3z+2i=0 hArr 3z = -2i hArr z = -2//3i`. Nesta altura, concluímos que se trata de um ponto, que neste caso é um imaginário puro, ou seja, a sua imagem geométrica encontra-se na parte negativa do eixo imaginário. Logo, se é um ponto, não pode definir uma reta. Espero ter-me feito entender!
17 de Novembro de 2018, 16h03
Mensagem de Tiago
Boa tarde professor,
No exercício 16, na alínea 2, para calcular a distancia entre Z1 e Z3, também não poderíamos utilizar o conhecimento que temos de vetores? Faria-mos Z3 - Z1 e depois calculava-mos o modulo (ou norma)? Obrigado.
17 de Novembro de 2018, 17h46
Mensagem de Vitor Nunes
Olá Tiago,
A resposta é afirmativa. A distância entre `Z_1` e `Z_3` também poderia ter sido calculada recorrendo à fórmula da distância entre dois pontos, ou em alternativa, utilizando o módulo de vetores. Como é óbvio o resultado final seria sempre o mesmo.
24 de Junho de 2021, 13h21
Mensagem de Manuel
No exercício 13, eu não entendi como fazer a alínea 13.1.
Fazendo a divisão, fica 6i. Daí não sei o que fazer para provar que ele é um imaginário puro.
24 de Junho de 2021, 14h40
Mensagem de Vitor Nunes
Olá Manuel,
Um número imaginário puro é um numero complexo da forma `z=a + bi`, em que, `a = 0`. Isto equivale a afirmar que, para um número ser considerado um imaginário puro, então terá que acontecer o seguinte: `Re(z) = 0` e `Im(z) in RR`. Portanto, ao verificar que o resultado é `6i` já estás a provar que é um imaginário puro.

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.




















 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 