Potências e radicais de números complexos.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

Uma potência de expoente natural é um produto de fatores todos iguais. O cálculo de potências de números complexos escritos na forma algébrica (exceto no caso dos números serem reais ou imaginários puros) é muito trabalhoso, mesmo usando a fórmula do Binómio de Newton. Por outro lado, a facilidade com que se multiplicam números na forma trigonométrica transmite-se, como é evidente, ao cálculo de potências de expoente natural.
Abraham de Moivre foi um matemático francês que emigrou para Inglaterra após a revogação do Édito de Nantes. Em Londres, trabalhou com Newton mas, por não ser inglês de nascimento, nunca conseguiu ser professor numa universidade. Tem, contudo, uma obre importante em Cálculo das Probabilidades e foi o primeiro a usar os complexos na Trigonometria. Em 1703 apresentou a fórmula que é conhecida hoje em dia por “fórmula de De Moivre”, que é utilizada para calcular potências e raízes de números complexos na forma trigonométrica.
ATENÇÃO
Nos novos programas de Matemática A, a forma de representar um número complexo na forma trigonométrica sofreu alterações. Já não se utiliza a notação: `z = rho.cis(theta)`.Em todas as aulas ou exercícios onde aparecer esta notação, ela deverá ser entendida como sendo: `z = |z| e^(i theta)`. Em todo o caso, o seu significado não se altera, continua a ser: `z = |z| (cos theta + i sin theta).`
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
25 de Maio de 2015, 14h28
Mensagem de Manuel António
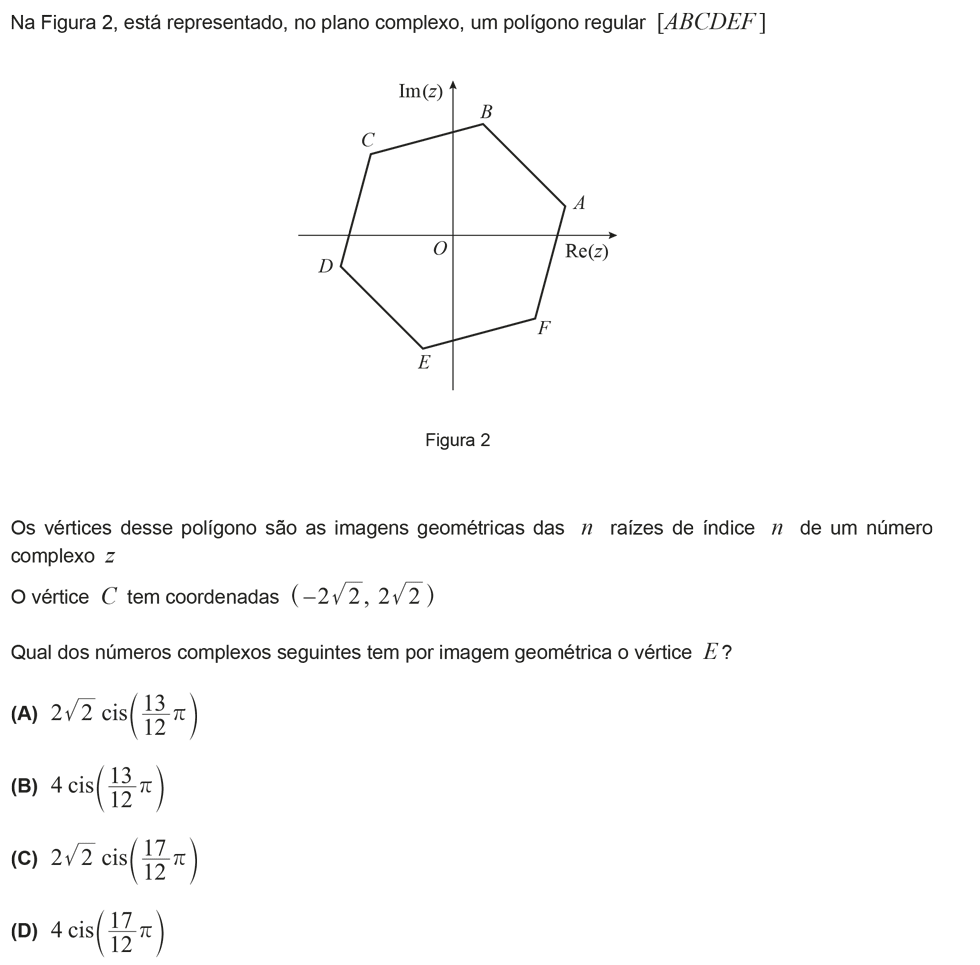
No exercício número 9 do Polígono Regular (Hexágono), a solução está errada, pois durante a resolução é escrito que a raiz quadrada de 4+4 é igual à raiz quadrada de 16 e portanto o valor da variável será 4.
25 de Maio de 2015, 14h45
Mensagem de Vitor Nunes
Olá Manuel,
Tens toda a razão, existe um erro na resolução, mas a solução está correta. Passo a explicar, quando o vídeo está no 1 minuto e 10 segundos existe um erro na resolução da raiz quadrada. Onde está `sqrt (4 + 4)` deveria estar `sqrt (8 + 8) = sqrt 16 = 4` e isto porque `(-2 sqrt 2)^2 + (2 sqrt 2)^2 = 4xx2 + 4xx2 = 8 + 8`.
Posto isto, a resposta certa, continua a ser a opção D.
Obrigado Manuel por ter reportado o erro. Bons estudos e boa sorte para o exame!

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.









 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 