Quadrados perfeitos e raiz quadrada.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

Um número é um quadrado perfeito se é o quadrado de um número inteiro não negativo. Por exemplo, o número `16` é um quadrado perfeito, porque `4^2 = 16`. Por outro lado, o número `22` não é um quadrado perfeito, porque não existe nenhum número inteiro, cujo quadrado seja `22`.
A raiz quadrada de um número é uma operação matemática, que permite encontrar o número que elevado ao quadrado, seja igual ao número que se encontra no interior da raiz. Por exemplo: `sqrt(25)=5`.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
03 de Dezembro de 2020, 19h16
Mensagem de Ana
O quadrado perfeito não é um número que dividido por dois tem de dar um numero inteiro?? Ali diz que 9 é um quadrado perfeito.
04 de Dezembro de 2020, 08h50
Mensagem de Vitor Nunes
Olá Ana,
Estás a cometer um pequeno erro. Um número é considerado um quadrado perfeito se a sua raiz quadrada for um número inteiro. Por outras palavras, tem de existir um número inteiro que multiplicado por ele próprio, vá dar esse número. Por exemplo, será que o número 36 é um quadrado perfeito? A resposta é sim, porque existe um número inteiro, neste caso o 6, que multiplicado por ele próprio vai dar 36. Espero que tenhas ficado esclarecida!
17 de Dezembro de 2020, 16h07
Mensagem de José Maria
Muito bom!
Uma sugestão: expliquem melhor a matéria com mais exemplos.
A minha dúvida é: podemos usar a raiz quadrada no dia a dia?
18 de Dezembro de 2020, 09h01
Mensagem de Vitor Nunes
Olá José,
Obrigado pela sugestão. Em relação à questão colocada, a resposta é sim. Existem várias situações do dia a dia em que o cálculo da raiz quadrada pode ser útil. Um dos melhores exemplos será o de descobrir o comprimento do lado de um terreno quadrado, desde que se conheça a sua área.
08 de Janeiro de 2021, 22h44
Mensagem de Lilia
Uma casa tem um jardim com 2187 metros quadrados de área. O jardim está dividido em três partes quadradas iguais. qual é a menor quantidade de rede, para vedar o jardim?
09 de Janeiro de 2021, 10h20
Mensagem de Vitor Nunes
Olá Lilia,
Vamos supor que temos um retângulo, que representa o jardim, cujo comprimento vou designar por `C` e a largura vou designar por `L`. Não conheço nem um nem outro. Mas, como pretendo dividir o retângulo em 3 quadrados iguais, então posso assumir que o comprimento vai ser igual a 3 vezes a largura. Logo `C = 3 xx L`. A área deste jardim pode ser calculada fazendo `C xx L`, que sabemos ser igual a 2187 metros quadrados, que é a mesma coisa que ter `3 xx L xx L = 2187`. Isto leva-nos a `3xxL^2=2187`, que por sua vez nos conduz a `L^2 = 2187 -: 3 hArr L^2 = 729`, logo `L = sqrt(729) hArr L = 27`. Agora que sabemos que a largura é 27 metros, também facilmente concluímos que o comprimento é o triplo, ou seja, 81 metros. Tendo em conta que já conhecemos o comprimento e a largura do jardim, para saber a quantidade de rede necessária para o cercar, bastar calcular o seu perímetro, O que nos leva a concluir que são necessários 216 metros de rede para vedar o jardim. Este tipo de exercício parece-me ser de dificuldade bastante elevada. Acho que não é necessário saber resolver algo assim tão complicado.
21 de Fevereiro de 2021, 01h29
Mensagem de Cláudia
Boa noite. Qual é a diferença entre √9/4 e √9:4? Ao tentar resolver a alínea 4 do exercício 1, em vez de ter recorrido à simplificação da fracção eu simplesmente dividi o numerador pelo denominador. Pergunto isto, porque entre fazer isto e a raiz quadrada de 9 a dividir por 4 tenho resultados distintos. Obrigada.
21 de Fevereiro de 2021, 09h12
Mensagem de Vitor Nunes
Olá Cláudia,
Em termos matemáticos, não existe diferença nenhuma entre uma coisa e outra. É absolutamente indiferente fazer de uma ou doutra forma. Mas ao utilizar uma calculadora existem diferenças. Isto porque ao fazer √9/4 a máquina de calcular efetua a operação tendo em conta que toda a fração está dentro da raiz quadrada, ou seja, na calculadora √9/4 é equivalente a `sqrt(9/4)`. Algumas máquinas de calcular mais modernas poderão apresentar o resultado desta operação na forma de fração, isto é, `3//2`. Se forem mais antigas, apresentam o resultado na forma de número decimal: `1,5`. Por outro lado, se utilizarmos a calculadora para efetuar esta operação √9:4, então primeiro ela calcula a raiz quadrada de 9 e só no fim é que divide esse resultado por 4. Logo, esta última operação é equivalente a `sqrt(9)/4`, tendo como resultado `3//4`.
04 de Junho de 2021, 20h34
Mensagem de Camila
Se um exercício contém, por exemplo, 3 x raiz quadrada de 6 ao quadrado. Como é que eu resolvo, se não existe raiz quadrada de 6 nos números inteiros?
05 de Junho de 2021, 09h42
Mensagem de Vitor Nunes
Olá Camila,
Se o enunciado pedir o resultado com algum tipo de arredondamento, então utilizamos a máquina de calcular para saber o valor da raiz quadrada de 6. Caso contrário deixamos ficar a raiz quadrada de 6, simplesmente não se calcula. Desse modo estamos a apresentar o resultado com o valor exato. Mas repara que no exemplo que apresentas, a raiz quadrada está ao quadrado, então a raiz pode cortar como o quadrado (porque é a operação inversa) e ficaria: `3 xx sqrt(6)^2 = 3 xx 6 = 18`

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.
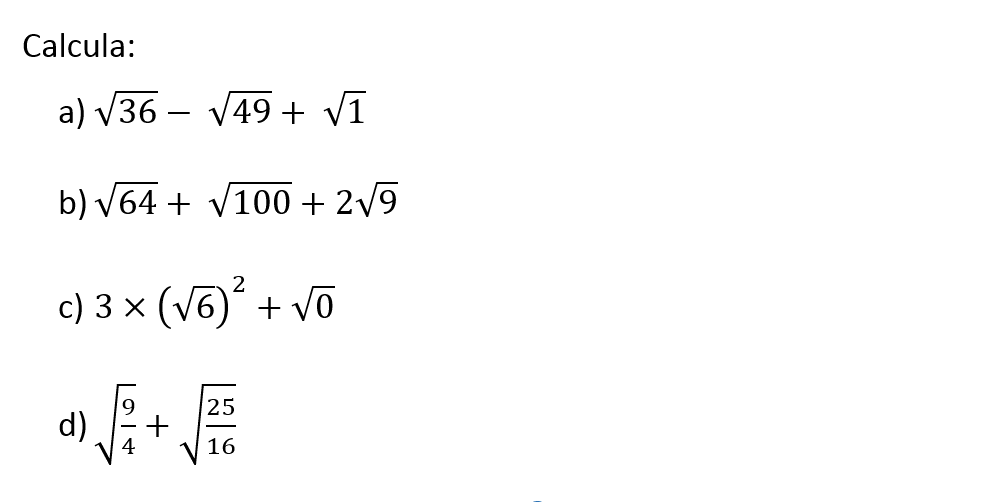
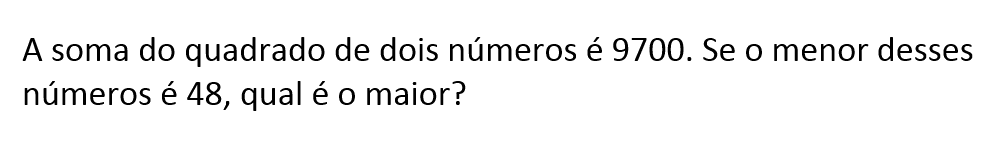



 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 