Pares ordenados e gráficos de funções.
Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução
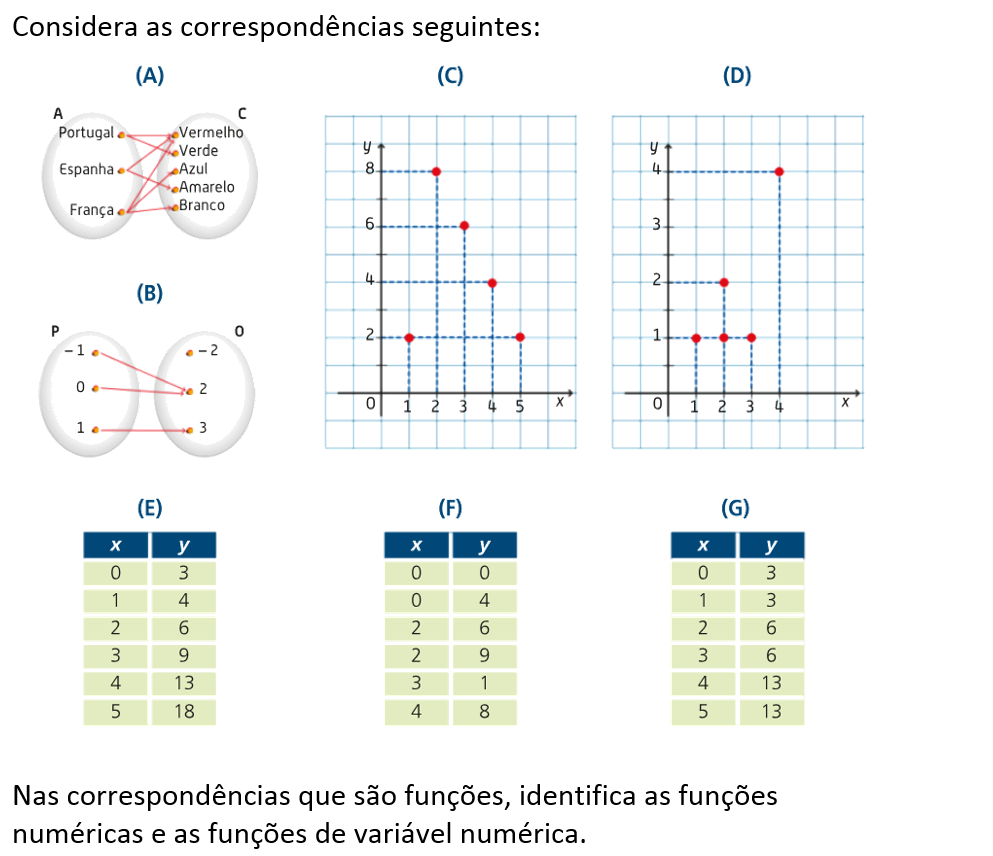
O gráfico de uma função `f: A -> B` é formado pelo conjunto de todos os seus pares ordenados `(x,y)`. Nestes pares ordenados o `x` pertence ao conjunto `A` e é designado por variável independente. O `y` pertence ao conjunto `B` e é designado por variável dependente.
A função recebe a designação de função numérica se os elementos do conjunto `B` forem apenas números. Se os elementos dos conjunto `A` forem apenas números, então recebe o nome de função de variável numérica. Por outro lado, se ambos os conjuntos `A` e `B` forem numéricos então diz-se uma função numérica de variável numérica.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
ATENÇÃO: Para poder utilizar esta opção terá que fazer Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
18 de Maio de 2023, 18h31
Mensagem de Mariana
Como saber se um gráfico é ou não uma função?
19 de Maio de 2023, 09h45
Mensagem de Vitor Nunes
Olá Mariana,
Primeiro tens que entender que uma função é uma correspondência entre dois conjuntos, em que a cada elemento do conjunto A corresponde um e só um elemento do conjunto B. Posto isto, num gráfico temos que analisar se a cada objeto (variável `x`) corresponde uma só imagem (variável `y`). A forma mais fácil de fazer isto, consiste em imaginar linhas na vertical, essas linhas só podem cruzar o gráfico da função num único local. Se essas linhas cruzarem o gráfico em mais do que um local então não se trata de uma função, porque isso significa que esse objeto tem mais que uma imagem. Eu sei que explicado por escrito pode não ser muito fácil de entender, mas espero que tenhas conseguido perceber a explicação.
29 de Março de 2024, 10h31
Mensagem de Álvaro
Bom dia sr. Vítor, a respeito do tipo de funções fiquei com uma dúvida. Que tipo de função seria se em ambos os conjuntos ( A e B) os elementos não forem números? Como exemplo estava a pensar num par de baile de finalistas:
Diogo------Mariana
José -------- Sofia
Que tipo de função seria esta, ou simplesmente não seria possível construir uma função a partir disto?
30 de Março de 2024, 18h17
Mensagem de Vitor Nunes
Olá Álvaro,
Uma função é uma correspondência entre elementos de dois conjuntos. A única condição para ser função é que a cada elemento do conjunto A corresponda um e só um elemento do conjunto B. Podem ser números, podem ser palavras, podem ser símbolos ou imagens é indiferente. Assim sendo, no seu exemplo, desde que cada um dos rapazes apenas convide para o baile uma única rapariga, então trata-se de uma função. Só não se pode chamar de função numérica. Penso que não existe nenhum nome específico para estes casos, pelo menos, que eu tenha conhecimento.
Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.
