Acontecimentos independentes.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

Num espaço `E`, sejam `A` e `B` dois acontecimentos, associados a uma experiência aleatória, tais que `P(A) != 0` e `P(B) != 0`. Diz-se que o acontecimento `A` é independente do acontecimento `B` se `P(A|B) = P(A)`.
Sendo `A` independente de `B`, também `B` é independente de `A`, o que permite que se fale em acontecimentos independentes. Sendo `A` e `B` dois acontecimentos independentes, tem-se `P(A nnB) = P(A).P(B)`
Embora os conceitos de acontecimentos incompatíveis e acontecimentos independentes sejam diferentes, podem gerar alguma confusão. Se dois acontecimentos (não vazios) são incompatíveis, não podem ocorrer em simultâneo. Então, a realização de um deles condiciona a realização do outro, o que mostra a sua não independência. Concluindo, acontecimentos incompatíveis, nunca são independentes; acontecimentos compatíveis podem ser, ou não, independentes.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
16 de Outubro de 2015, 22h08
Mensagem de IML
Olá!
Gostaria de saber porque é que as outras 3 opções do exercício nº 1 não são possíveis. E como é que a partir do enunciado se chega a opção correta se não tivéssemos hipóteses. Agradeço resposta.
E agradeço toda a ajuda que tem fornecido através das aulas. Muito obrigado.
16 de Outubro de 2015, 22h46
Mensagem de Milita
No exercício 3, não poderíamos a partir da expressão do ponto 3 do enunciado iguala-lá à probabilidade do contrário do acontecimento A vezes a probabilidade do contrário do acontecimento B, visto que o contrário de A e B são independentes se A e B são independentes e eles são, como diz no enunciado?
19 de Outubro de 2015, 12h23
Mensagem de Vitor Nunes
Olá IML,
O enunciado pergunta "Qual das afirmações é necessariamente verdadeira?". O nosso foco deverá ir para a palavra necessariamente. Sabendo que os acontecimentos `A` e `B` são independentes eu não consigo afirmar que as opções A) B) e C) do exercício 1 são falsas, mas também não consigo afirmar que são verdadeiras. Podem ser, podem não ser. A única coisa de que temos a certeza é que a opção D) é verdadeira, pelas razões que são explicadas no vídeo. Espero ter ajudado!
19 de Outubro de 2015, 12h42
Mensagem de Vitor Nunes
Olá milita,
Não, a fórmula que referes não existe, logo não pode ser aplicada. E mesmo que fosses por esse caminho, como não conheces a probabilidade do acontecimento `B` então também não conheces a probabilidade do acontecimento contrário de `B`, assim sendo, indo por essa via, ias ter a um beco sem saída. A única forma de resolver este exercício (pelo menos que eu conheça) é aquela que está explicada no vídeo com a resolução. Boa sorte para os estudos!
16 de Junho de 2016, 23h02
Mensagem de ios
O exercício 3 também poderia ser resolvido duma outra forma, isto é, a probabilidade de b seria igual a probabilidade de a interseção com b a dividir pela probabilidade de a. Desta forma a partir do axioma, p de a união com b é igual a p de a+p de b-p de a interseção com b, sendo que p de a união com b é 1-0.48, substituíamos p de b, no axioma por a probabilidade de a interseção com b a dividir pela probabilidade de a. Obtiamos o mesmo resultado.
17 de Junho de 2016, 08h36
Mensagem de Vitor Nunes
Olá ios,
Tive alguma dificuldade em seguir o teu raciocínio, mas se deu o mesmo resultado é provável que a resolução que sugeres também esteja correta. Na matemática, existem várias formas de chegar ao resultado final, é possível que a resolução que eu sugiro no vídeo nem sequer seja a mais fácil. Desde que os alunos cheguem ao resultado e justifiquem corretamente, a resolução é aceite. É esta a beleza da matemática!
30 de Outubro de 2017, 19h48
Mensagem de Jacinto
Preciso de ajuda: numa caixa tem 2 moedas falsas e 10 verdadeiras. retirou-se ao acaso uma a uma, qual é a probabilidade de as primeiras a sair serem as falsas?
01 de Novembro de 2017, 07h00
Mensagem de Vitor Nunes
Olá Jacinto,
Normalmente só respondo a perguntas diretamente relacionadas com os exercícios, mas como estou com tempo vou dar uma ajuda! Pretende-se que as primeiras duas moedas extraídas sejam falsas, logo a probabilidade da primeira ser falsa é `2/12`, existem 2 casos favoráveis em 12 possíveis. Já a probabilidade da segunda também ser falsa é `1/11`, uma vez que existe 1 caso favorável em 11 possíveis. Para obter a probabilidade pedida, basta fazer `2/12 xx 1/11`. Espero que tenhas percebido.
06 de Dezembro de 2017, 11h13
Mensagem de Luis Sousa
Bom dia, este exercício está no manual do 12 ano - Expoente 12, Matemática A, Vol I, exercício nº37, página 125:
Sejam E um conjunto finito, não vazio, P uma probabilidade no conjunto P(E) e A e B dois acontecimentos em E, tais que A e B são acontecimento equiprováveis e independentes. Prova que P(A U B) = P(A) [2-P(A)]
Obrigado pela ajuda,
Atentamente, Luís Sousa
07 de Dezembro de 2017, 08h21
Mensagem de Vitor Nunes
Olá Luís,
Não costumo resolver exercícios dos manuais, mas aqui fica a resolução:
Tendo em conta que `A` e `B` são acontecimentos equiprovaveis então `P(A) = P(B)`.
Tendo em conta que `A` e `B` são acontecimentos independentes então `P(A nn B) = P(A) xx P(B)`.
`P(A uu B) = P(A) [2 - P(A)] hArr` `P(A) + P(B) - P(A nn B) = 2P(A) - P^2(A) hArr` `P(A) + P(B) - P(A) xx P(B) = 2P(A) - P^2(A) hArr` `P(A) + P(A) - P(A) xx P(A) = 2P(A) - P^2(A) hArr` `2P(A) - P^2(A) = 2P(A) - P^2(A)`.

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.















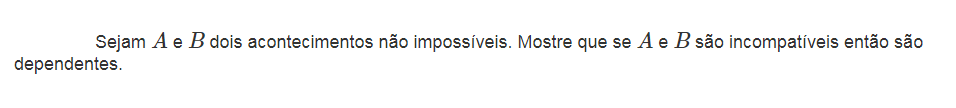
 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 