Arranjos e Combinações. Cálculo Combinatório.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

Dado um conjunto com `n` elementos, o número total de sequências de `p` elementos distintos, escolhidos de entre os `n` elementos, com `p <= n`, representa-se por ` text()^nA_p` e lê-se número de arranjos simples, ou sem repetição, de `n` elementos, tomados `p` a `p`.
Dado um conjunto com `n` elementos, o número total de sequências de `p` elementos, repetidos ou não, escolhidos de entre os `n` elementos, representa-se por ` text()^nA’_p` e lê-se número de arranjos completos, ou com repetição, de `n` elementos, tomados `p` a `p`.
Dado um conjunto com `n` elementos, chama-se combinação dos elementos desse conjunto, a qualquer dos seus subconjuntos. O número total de combinações com `p` elementos escolhidos de entre `n` representa-se por ` text()^nC_p`.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
19 de Dezembro de 2014, 19h13
Mensagem de Miguel
Tive muitas dúvidas nesta matéria de probabilidades porque não sei qual utilizar, se é arranjo simples, completo ou combinações. Mesmo depois de ver o vídeo com as explicações da matéria parece que nunca acerto.
21 de Dezembro de 2014, 14h55
Mensagem de Rui
É assim Miguel, só tens que analisar o contexto do problema. Se for para contar o número de conjuntos que é possivel formar em que a ordem não interessa, utilizas a combinação. Caso a ordem interesse, se puder haver repetição dos elementos do conjunto é um arranjo completo, se não puder haver repetição é um arranjo simples.
De inicio esta matéria das probabilidades também me fazia muita confusão, mas depois de resolver vários exercícios comecei a encaixar melhor.
06 de Março de 2015, 16h33
Mensagem de José Reis
a) Como achar as chaves possíveis do euro-milhões?
b) Como conseguir que o computador dite chaves do euro-milhões por exemplo de segundo a segundo?
grato antecipadamente
Reis
07 de Março de 2015, 01h31
Mensagem de Vitor Nunes
Olá José,
Normalmente só aceito que o fórum seja utilizado para colocar dúvidas sobre os exercícios propostos. Mas como a questão colocada é interessante vou abrir uma exceção.
Em relação à alínea a) que consiste em saber quantas chaves existem do euromilhões, não é difícil de calcular. Para o prémio máximo temos que acertar em 5 números (de um total de 50) e em 2 estrelas (de um total de 11), assim sendo: `text()^50C_5 xx text()^11C_2 = 116.531.800`.
Não percebi a alinea b).
19 de Março de 2015, 16h02
Mensagem de Reis
Grato pela prontidão da vossa resposta a alínea a;
Acerca da alínea b o que eu gostava de saber era se o computador tem alguma formula - por ex: no exel - de ditar chaves(conjuntos) de 5 números em 50 e conjuntos de 2 em 11?
Mais uma vez grato antecipadamente
Reis
20 de Março de 2015, 08h06
Mensagem de Vitor Nunes
Olá José,
Conheço particularmente bem o Excel, no entanto, não conheço nenhuma maneira de gerar números aleatórios de acordo com os requisitos que pedes.
Isso pode ser feito facilmente, no computador, usando uma linguagem de Programação como Delphi, C++ ou PHP, mas para isso terias que perceber de programação. Lamento não poder ajudar mais.
31 de Março de 2015, 16h27
Mensagem de José Reis
Agradeço e gosto muito do vosso site;
Parabéns, Pascoa Feliz e um enorme abraço
06 de Abril de 2015, 20h25
Mensagem de MadalenaT
Boa tarde, gostaria de saber se o exercício nº 14 pode ser resolvido com arranjos?
Ex.: 5 nPr 2 + 5 nPr 4 = 140
07 de Abril de 2015, 10h17
Mensagem de Vitor Nunes
Olá Madalena,
A resposta é sim. O exercício 14 pode ser resolvido com arranjos simples, exatamente da forma como indicaste, como no fundo, a ordem das cores interessa, o teu método acaba por ser bem mais simples que o meu. Nesta matéria do Cálculo Combinatório existem sempre várias formas de chegar ao resultado correto. Frequentemente os alunos optam por uma forma de resolução diferente daquela que é sugerida pelo professor, e desde que o raciocínio esteja correto, todos os métodos são válidos.
07 de Abril de 2015, 18h50
Mensagem de MadalenaT
Prof. Vitor Nunes muito obrigada pela explicação.
Cumprimentos.
10 de Novembro de 2015, 17h02
Mensagem de Ana
Tenho dúvidas no exercício 5 pois não percebi porque é que se usa a combinação e não o arranjo completo, uma vez que existe a repetição do numero 5
11 de Novembro de 2015, 10h29
Mensagem de Vitor Nunes
Olá Ana,
É usada a Combinação e não os arranjos completos porque a ordem não interessa. Repara que estamos a repetir três vezes o algarismo 5. Como é sempre o mesmo algarismo que se repete, não importa a ordem em que essa repetição é feita. Se por exemplo quiseres fazer uma pizza e dos cinco ingredientes disponíveis for necessário escolher três, a ordem dessa escolha não interessa, uma vez que a pizza é sempre a mesma! Nos casos em que a ordem não interessa usa-se sempre a Combinação.
12 de Novembro de 2015, 17h59
Mensagem de José Martins
Boa tarde,
Tenho uma dúvida que gostaria que me ajudassem, gostaria de saber quantas combinações existem em 4 jogos de voleibol (não há empates):
- Jogo A : Vitória ou Derrota
- Jogo B : Vitória ou Derrota
- Jogo C : Vitória ou Derrota
- Jogo D : Vitória ou Derrota
Se existisse uma espécie de totobola assim, quantas são as combinações possíveis para acertar no resultado dos 4 jogos?
Cumprimentos
13 de Novembro de 2015, 09h09
Mensagem de Vitor Nunes
Olá José,
Por norma, apenas respondo a dúvidas que estejam relacionadas com os exercícios propostos, mas vou abrir uma exceção. Cada jogo só tem dois resultados possíveis, como temos quatro jogos a serem disputados, o total de combinações possíveis de resultados é de `2^4=16`. Para garantir que acertavas na previsão de todos os resultados dos quatro jogos teriam que ser preenchidos 16 boletins de Totobola diferentes. Espero ter ajudado, boa sorte!
07 de Dezembro de 2015, 14h54
Mensagem de Ana
Boa Tarde,
Vou ter teste de matemática e estou preocupada porque não percebo quando utilizar arranjos, permutações ou combinações. Sei em que cada situação se deve utilizar qual no entanto quando estou perante um exercício não o consigo perceber qual utilizar. Existem algumas palavras chave que me possam ajudar?
09 de Dezembro de 2015, 21h28
Mensagem de Vitor Nunes
Olá Ana,
Essa é uma dúvida muito comum entre os alunos e só se resolve com muito treino. Não existe nenhuma palavra chave a que tenhas que estar atenta, tens apenas que ler o enunciado com muita atenção e tentar perceber pequenos pormenores: Se a ordem não for importante então trata-se de uma combinação. Se a ordem for importante e não houver repetição então estamos na presença de um arranjo simples. Se nenhum elemento ficar de fora é uma permutação. Boa sorte para o teste!
10 de Outubro de 2016, 19h21
Mensagem de Luis Gonçalves
Olá. Aqui há dias deparei-me com o seguinte exercício e ainda não o consegui resolver!!!!
"Quantos números naturais de três algarismos diferentes se podem escrever não utilizando o algarismo 2 nem o algarismo 5." Aguardo resposta. Cumprimentos!
12 de Outubro de 2016, 15h05
Mensagem de Vitor Nunes
Olá Luís,
Já mencionei em mensagens anteriores, que tenho por hábito responder apenas a questões relacionadas com os exercícios presentes na página. Mais uma vez, vou abrir uma exceção. Este exercício podia ser resolvido com a utilização das Combinações, mas vou utilizar a Regra do Produto (também conhecido por Principio da Multiplicação). Do enunciado, retiramos logo a informação que temos 8 opções disponíveis. No entanto, nenhum número pode começar por zero, assim sendo, no caso do primeiro algarismo temos apenas 7 opções de escolha. No segundo algarismo temos novamente 7 opções de escolha, porque voltamos a ter o zero disponível mas não podemos usar o mesmo algarismo já utilizado anteriormente. Para o terceiro algarismo temos 6 escolhas possíveis. O resultado final é então: `7xx7xx6 = 294`.
18 de Janeiro de 2017, 22h51
Mensagem de João Gregório
Boas,
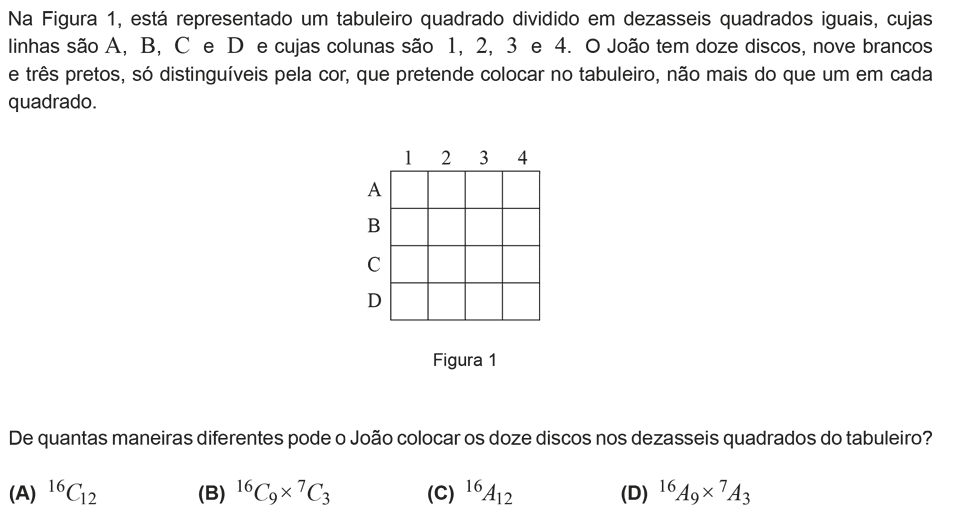
No exercício nº8 porque fez a conta separando os brancos dos pretos: 16C9 X 7C3, e não somou as peças todas dando o resultado 16C12? Obrigado pela atenção.
19 de Janeiro de 2017, 09h17
Mensagem de Vitor Nunes
Olá João,
Não se pode somar tudo, porque as peças não são todas iguais. Umas são pretas e outras são brancas. Como são peças diferentes, colocar uma peça de uma cor ou de outra, faz com que o tabuleiro tenha um aspeto diferente. Assim sendo, para contar de quantas formas podemos colocar as peças, temos que contar separadamente.
05 de Julho de 2017, 15h05
Mensagem de Inês M
Boa tarde professor,
Desculpe o incomodo, mas gostaria de perguntar porque é que, no exercício 5, a resposta não é 5C3 x 4C2. Não consigo perceber o porquê de a última expressão ser representada por arranjos (com repetição) e não combinações... Porque é que interessa a ordem? Obrigada.
06 de Julho de 2017, 14h40
Mensagem de Vitor Nunes
Olá Inês,
Não é incomodo nenhum, tenho todo o prazer em prestar esclarecimentos. Vamos supor o seguinte: o algarismo 5, fica na primeira, terceira e quinta posição, assim obtemos 5_5_5. Aqui claramente a ordem não interessa, porque se trocarmos o 5 de lugar, o número é o mesmo. Vou agora escolher outros dois algarismos, por exemplo o 6 e o 7. Repara que pode ficar 56575 ou 57565, isto se trocarmos o 6 e o 7 de lugar. Logo, neste caso a ordem interessa! Assim sendo, trata-se de um arranjo e não de uma combinação. Neste caso é com repetição, porque o enunciado não refere, que os restantes algarismos não possam ser repetidos. Espero que tenhas percebido.
08 de Julho de 2017, 11h41
Mensagem de Inês M
Já entendi, muito obrigada! Tem sido o meu "melhor amigo" enquanto estudo para a 2ª fase! Cumprimentos e continuação de um ótimo trabalho.
09 de Julho de 2017, 05h34
Mensagem de Artur
Boa noite!
No exercício 10, como estamos a falar de 6 números 2, e como cada número altera o resultado consoante a sua posição, não estaremos a falar de um arranjo ao invés de uma combinação? Obrigado!
09 de Julho de 2017, 18h06
Mensagem de Vitor Nunes
Olá Artur,
Em relação à escolha do local em que fica o algarismo 2, trata-se de uma combinação. Repara que escolhemos 6 posições diferentes para colocar o número 2. Depois dessa escolha estar feita, não importa as trocas que possas fazer entre esses 6 algarismos, uma vez que é sempre o mesmo. Estamos a falar de trocar os 6 algarismos 2 entre si, não estamos a falar em mudá-los de posição. Espero que me tenha feito entender.
06 de Dezembro de 2019, 15h19
Mensagem de Ana
Olá,
Eu queria saber se num exercício em que me pede as maneiras diferentes de eleger o delegado, o subdelegado e o suplente eu posso fazer 20C1 × 19C1 × 18C1, uma vez que eu fiz dessa maneira e afirmaram que tinha que fazer 20A3 pois a ordem interessa, contudo o resultado está correto.
Obrigado.
06 de Dezembro de 2019, 17h17
Mensagem de Vitor Nunes
Olá Ana,
É um questão interessante. Mais do que analisar o resultado final, que é igual (podia ser igual e ser apenas coincidência), importa analisar o raciocínio que te levou a essa escolha. Na tua maneira de pensar, calculo que pegaste numa turma com 20 alunos e foste escolher 1 para ser o delegado. De seguida, dos 19 que sobraram, foste escolher 1 para ser subdelegado e assim por diante. Apesar de não ser a forma mais rápida de chegar à solução do problema, o raciocínio está certo. Assim sendo, eu aceitaria a tua resposta como sendo válida.
17 de Abril de 2020, 22h27
Mensagem de Henrique
No exercício 4, não percebo o porquê de se usar combinações e não arranjos, visto que num código interessa a ordem dos seus elementos.
18 de Abril de 2020, 12h47
Mensagem de Vitor Nunes
Olá Henrique,
Claro que num código secreto a ordem dos seus elementos é importante. Mas repara que no exercício 4 estou a utilizar combinações porque os elementos são iguais! Por exemplo, eu quero colocar 4 vezes a letra "`a`", utilizo combinações porque é sempre a mesma letra, logo a ordem não interessa. Mas se tivesse que colocar 4 letras diferentes, claro que teria que utilizar arranjos em vez de combinações.
10 de Junho de 2020, 00h41
Mensagem de André
Boa noite,
Conseguem-me ajudar com este exercício?
Uma caixa contém 5 bolas amarelas e 3 bolas vermelhas. Extraem-se ao acaso três bolas da caixa. Determine a probabilidade de saírem duas bolas amarelas e uma vermelha.
11 de Junho de 2020, 09h00
Mensagem de Vitor Nunes
Olá André,
Não costumo responder a perguntas propostas pelos alunos. Mas como até tenho algum tempo disponível, vou abrir uma exceção. Como queremos extrair 2 bolas amarelas e 1 vermelha, basta multiplicar estas probabilidades, logo: `5/8xx4/7xx3/6`. Repara que, como não há reposição, à medida que realizamos a extração, o número de bolas na caixa vai diminuindo. Contudo, só isto não é suficiente, porque as bolas não precisam de ser extraídas exatamente por esta ordem. Assim sendo, resta-nos multiplicar o resultado anterior, pelo número de formas diferentes de extrair as 3 bolas pretendidas (AAV, AVA, AAV) que é 3.
28 de Março de 2024, 19h20
Mensagem de Marcelo
Saudações matemáticas Vítor!
No ex.12 alínea c, diz "de modo a que saiam apenas 2 raparigas no início...". Interpretei que no início eu deveria considerar apenas 2 raparigas e para os 4 cartões restantes, era possível considerar raparigas e também rapazes, ou seja, arranjos completos de 23 alunos, 4 a 4. Porém, foi considerado apenas 2 raparigas para os 6 cartões e foi calculado para as 4 casas restantes arranjos completos de 12 (rapazes) 4 a 4.
Você não acha que o texto gerou dupla interpretação?
30 de Março de 2024, 18h05
Mensagem de Vitor Nunes
Olá Marcelo,
Voltei a ler o texto e talvez tenha razão. Se calhar o enunciado deveria ser um pouco mais claro. Ainda assim, ao resolver o exercício, eu interpreto o seguinte texto "... apenas 2 raparigas...", como sendo a indicação que não deverão sair mais raparigas. No meu entender, a palavra "apenas" é uma condição que nos diz que o resto da extração deverá ser constituída só por rapazes. Mas concordo que o enunciado não se deve prestar a este tipo de dúvidas. Deve ser sempre o mais claro possível.

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.












 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 