Triângulo de Pascal. Construção e interpretação.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

É atribuido a Blaise Pascal a invenção da primeira calculadora mecânica, conhecida pelo nome de pascalina. No entanto, Pascal assim como o matemático italiano Tartaglia, têm o seus nomes associados ao conhecido Triângulo de Pascal. Ambos recorreram a este triângulo numérico na realização de muitos dos seus trabalhos. São várias as referências documentais a este triângulo por civilizações ainda mais antigas, algumas cerca de 2000 anos antes de Pascal. Existem várias relações numéricas que se podem obter a partir do Triângulo de Pascal, uma delas são os termos da conhecida sucessão de Fibonacci.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
19 de Dezembro de 2014, 19h00
Mensagem de Ana
Não venho colocar nenhuma dúvida, apenas agradecer as suas explicações de matemática e os exercícios resolvidos que me ajudaram a perceber melhor o funcionamento do triângulo de pascal.
21 de Dezembro de 2014, 14h50
Mensagem de Vitor Nunes
Olá Ana,
Obrigado pelas palavras de agradecimento.
Votos de boas notas!
03 de Janeiro de 2015, 11h31
Mensagem de Teresa
Eu também achei este site muito útil. Já utilizava outros mas acho que aqui os assuntos estão mais organizados e como todos os exercícios de matemática que estão disponíveis têm a resolução em vídeo isso ajuda-nos imenso quando não sabemos muito bem como começar. As vezes basta vermos os primeiros passos da resolução para saber logo qual é o caminho a seguir. Adorei as explicações espero que possam continuar a acrescentar mais e mais exercícios. Estou confiante numa boa nota no exame nacional.
06 de Janeiro de 2015, 09h41
Mensagem de Vitor Nunes
Olá Teresa,
Fico contente por poder ajudar a esclarecer as vossas dúvidas em matemática.
Boa sorte para o Exame Nacional!
04 de Setembro de 2016, 20h07
Mensagem de Jonathan Nascimento
Muito obrigado estou no 2º ano e tinha que procurar 15 exemplos de exercícios com o triangulo de pascal e explicar para a turma, e aqui consegui tudo o que precisava, muito obrigado, vcs vão longe desse jeito.
09 de Janeiro de 2017, 21h21
Mensagem de Alex
Na 12º pregunta era possivel igualar o nC2 a 55 e resolver como equação através da formula (n)!/(n-p)!p! ?
10 de Janeiro de 2017, 09h30
Mensagem de Vitor Nunes
Olá Alex,
A resposta é sim. No meu entender dá um pouco mais de trabalho do que a resolução proposta no vídeo, mas é perfeitamente viável. Resolvendo essa equação obtens o valor de `n` e rapidamente ficas a saber qual é o penúltimo elemento dessa linha do Triângulo de Pascal. Um das coisas que eu gosto na matemática é que não existe um só caminho para chegar à solução de um problema. Cada um de nós pode escolher um percurso diferente e chegar ao mesmo destino!
15 de Março de 2019, 11h57
Mensagem de Hadla
Olá! Boa tarde!
A primeira linha é chamada linha 0 (zero), a segunda linha 1, e assim por diante? Fiquei confusa nessa parte e tenho receio de errar alguma coisa devido à interpretação. Desde já agradeço a atenção, e aproveito para dizer que estas explicações têm me ajudado imenso a perceber a matéria :)
15 de Março de 2019, 16h45
Mensagem de Vitor Nunes
Olá Hadla,
Sim aquilo que acabaste de afirmar está certo! No Triângulo de Pascal a primeira linha é a linha zero, a segunda linha é a linha um e por aí fora. Qualquer dúvida que tenhas relacionada com os exercícios que disponibilizamos, não hesites em colocar. Estamos aqui para ajudar!
08 de Maio de 2020, 23h47
Mensagem de Joana
Olá Vitor,
A resolução do exercício 10 foi dúbia para mim. Pois segundo a minha lógica, num universo de 9 elementos, o denominador seria originalmente 9 e não uma combinação de 9, 2 a 2 (36). Pode explicar-me melhor? Obrigada.
09 de Maio de 2020, 08h55
Mensagem de Vitor Nunes
Olá Joana,
Num universo de nove elementos, o número de escolhas possíveis seria 9 se estivéssemos a escolher apenas um elemento. Mas repara que no exercício 10, menciona que deverão ser escolhidos ao acaso dois desses nove elementos. Logo, como a ordem não interessa, isso resulta numa combinação de 9 elementos, escolhida dois a dois. Isso significa que consigo escolher 36 diferentes conjuntos de dois elementos. Espero ter ajudado.
15 de Novembro de 2024, 14h24
Mensagem de Ayrton
Olá!
Professor, no exercicio 17, a enésima linha não deveria ser a linha n. Deveria ser nC2 = 171, não?
Obrigado e bom final de semana.
18 de Novembro de 2024, 10h46
Mensagem de Vitor Nunes
Olá Ayrton,
No vídeo está explicado, de forma bastante clara, que o segundo elemento da 5ª linha do triangulo de Pascal é `text()^4C_1`. Isto porque a contagem das linhas começa no número 1, mas as combinações começam no zero. Assim sendo, o terceiro elemento da n-ésima linha é `text()^(n-1)C_2`.

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.
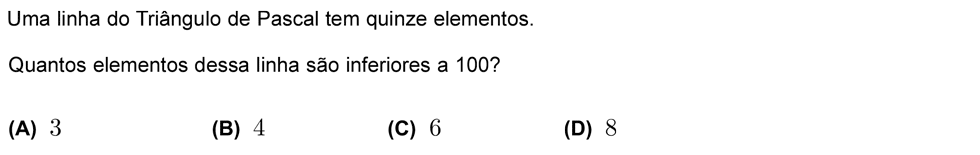


















 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 