Limites laterais. Limites num ponto.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

Já no 11º ano tinha sido abordado o conceito de limite, quer a propósito de assíntotas dos gráficos das funções racionais, quer a propósito do cálculo da derivada de uma função num ponto, como limite da taxa média de variação. Vai-se agora dar inicio ao estudo dos limites na função exponencial e na função logarítmica. O conceito de limite é fundamental no Cálculo Infinitesimal e é por isso que vai ser aprofundado e formalizar o que ele representa.
Já na Grécia antiga foram utilizados os conceitos de limite e de infinito, mesmo sem qualquer referência aos mesmos. Tem-se por exemplo, o processo utilizado por Arquimedes na determinação do comprimento de uma circunferência de raio 1, recorrendo a pares de polígonos regulares, um inscrito e outro circunscrito à circunferência. Quanto maior o número de lados dos polígonos utilizados mais os respetivos perímetros se aproximavam do valor do comprimento da circunferência. Foi com o matemático francês Lagrange que surgiu a primeira “Teoria de funções de variável real” com aplicação a uma grande variedade de problemas de Álgebra e Geometria. Foi ele o criador do símbolo `f’(x)` para a derivada.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.
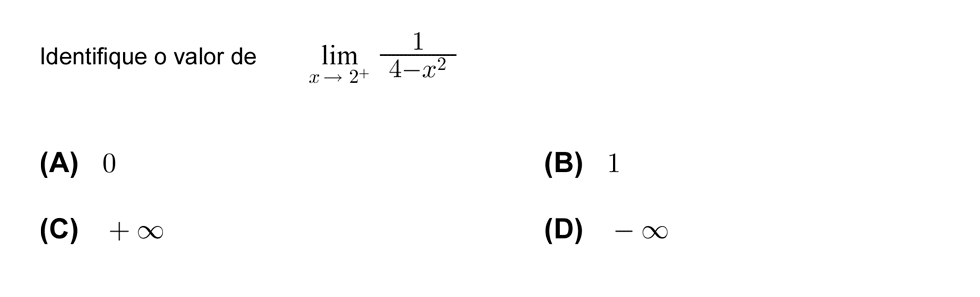

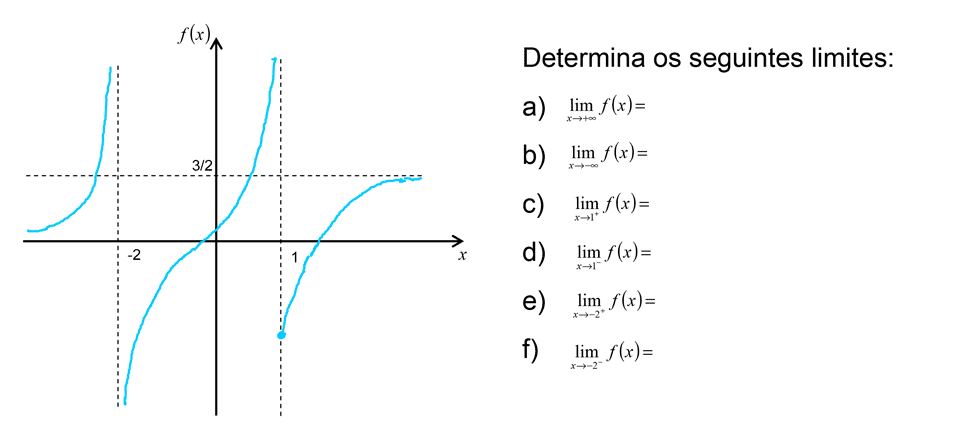
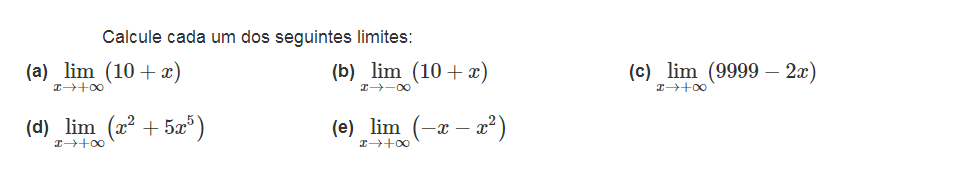
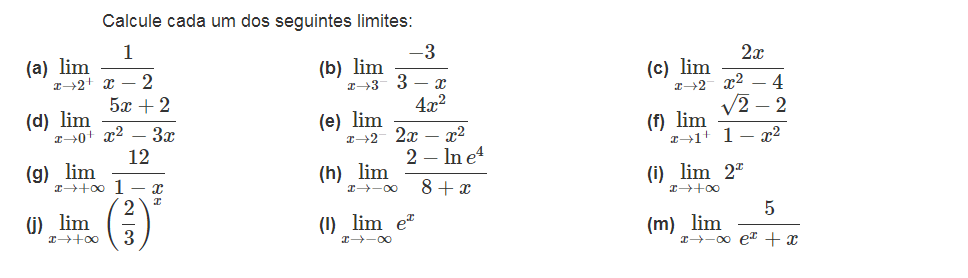
 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 