Cálculo de limites sem indeterminação.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

O cálculo dos limites vai ser aplicado ao estudo da continuidade de uma função em pontos de acumulação do domínio, na identificação de assíntotas do gráfico de funções racionais e não racionais e no cálculo da derivada de uma função num ponto a partir da taxa média de variação. Se a máquina de calcular pode ser útil para estabelecer conjeturas relativas à existência e valor de um limite, é importante conhecer e saber aplicar ferramentas analíticas que permitam sustentar as hipóteses formuladas.
Explicação da matéria
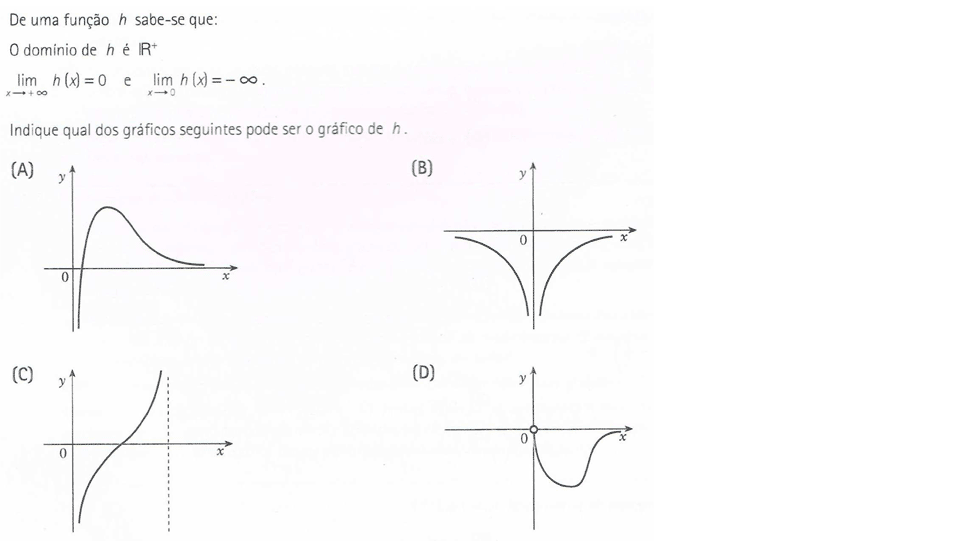
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
28 de Agosto de 2016, 17h15
Mensagem de Rui Silva
Boa tarde. A duvida é a seguinte: no exercicio n°10, quando diz que y=-4 é assimptota da função. Essa assimptota não atravessa os quadrantes 3 e 4 do grafico? Impedindo logo ali que o Contradominio da funçao fosse ]-inf, 3] ?? Obrigado pela atenção! Este site é excelente!!!!
30 de Agosto de 2016, 10h36
Mensagem de Vitor Nunes
Olá Rui,
É verdade que a reta `y=-4`, sendo uma reta horizontal, "atravessa" o terceiro e quarto quadrante. Mas, isso em nada interfere com a forma como é calculado o contradomínio da função. Sabemos apenas, que por definição, os valores da função se aproximam dessa reta, ou seja, da imagem `-4` quando os objetos tendem para mais ou menos infinito. Acontece, que isso não impede que a função tenha uma imagem `-4`, ou que o contradomínio esteja definido quer por cima, quer por baixo desse valor.
13 de Fevereiro de 2017, 22h01
Mensagem de Eugênia
Quando nos aparece em exercícios de limites uma constante a dividir por zero, como sabemos se dá mais infinito ou menos infinito? Ou quando é uma constante sobre infinito, como sabemos se dá zero mais ou zero menos?
14 de Fevereiro de 2017, 07h46
Mensagem de Vitor Nunes
Olá Eugênia,
No cálculo de limites, se aparecer um exercício em que o numerador é uma constante e o denominador é zero, é necessário ver se é um zero mais ou zero menos. Normalmente isso é feito estudando os limites laterais. Existem imensos casos diferentes e é difícil estar aqui a falar de cada um deles. Podes utilizar a seguinte estratégia: se por exemplo estiveres a calcular um exercício em que `x->2^+` então substitui o `x` por `2,1` e verifica se dá positivo, nesse caso trata-se de `0^+`, caso contrario é um `0^-`. Se `x->2^-` então substitui o `x` por `1,9` e faz a mesma verificação anterior. No caso do denominador tender para infinito, trata-se também de analisar, por um processo análogo, se é um infinito positivo ou negativo. Espero ter ajudado!

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.






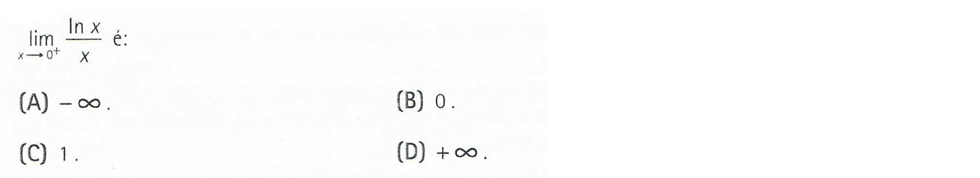
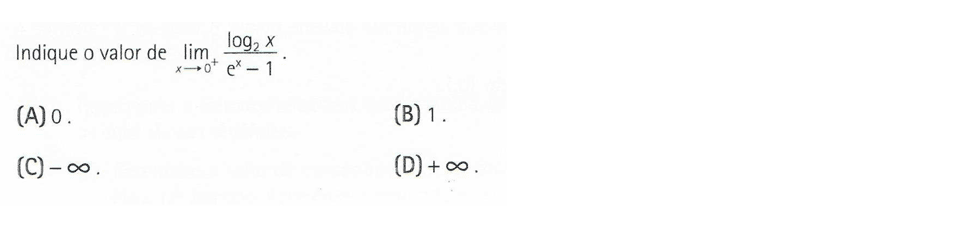


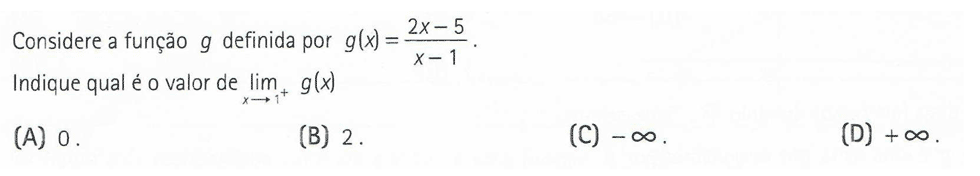




 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 