Taxa de variação média e instantânea.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

A variação de uma função `f` num intervalo `[a,b]`, do seu domínio, é dada por: `f(b) – f(a)`.
A Taxa Média de Variação de uma função `f` no intervalo `[a,b]` é dada por `TMV=( f(b) – f(a))/(b-a)`.
A Taxa Média de Variação de uma função `f` no intervalo `[a,b]` representa geometricamente o declive de reta definida pelos pontos `AB`. Em física, a taxa média de variação está associada à velocidade média, num certo intervalo de tempo.
A Taxa de Variação de uma função `f` real de variável real, num ponto, caso exista é calculada através da seguinte fórmula: `f'(x_0)=lim_(x->x_0)(f(x)-f(x_0))/(x-x_0)` ou `f'(x_0)=lim_(h->0)(f(x_0+h)-f(x_0))/h`.
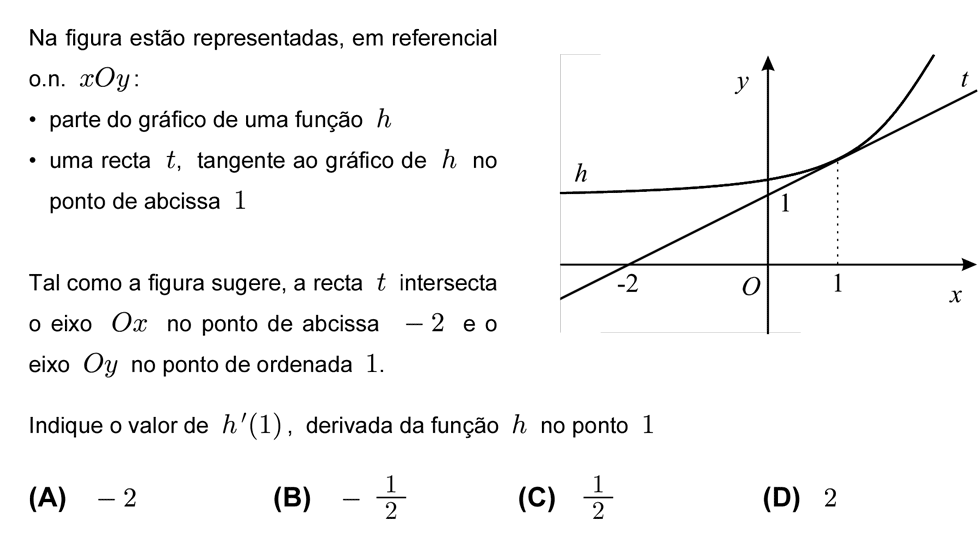
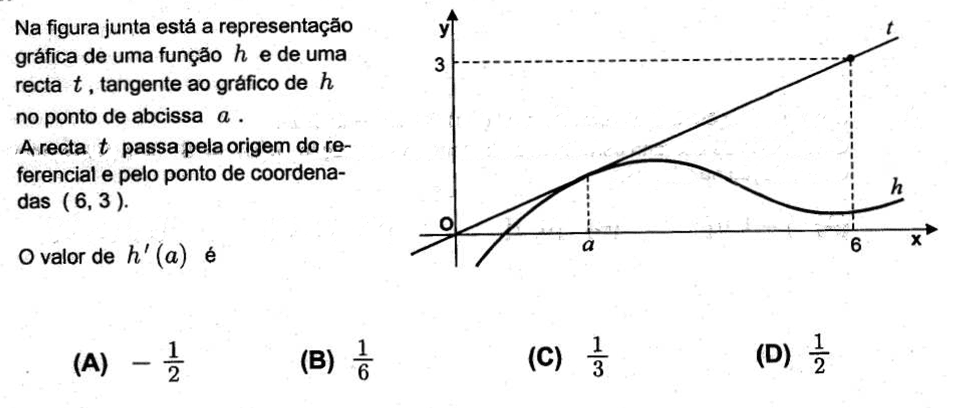
A Taxa de Variação de uma função num ponto, ou seja, `f’(x_0)`, representa geometricamente o declive da reta tangente ao gráfico de `f` no ponto de abcissa `x_0`. Em física, esta taxa de variação está associada à rapidez instantânea, ou em linguagem comum, velocidade instantânea.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
08 de Abril de 2015, 15h45
Mensagem de Fernanda
Ainda não consegui perceber para que é que serve esta taxa e qual a diferença em relação à derivada. É a mesma coisa, ou taxa de variação média é uma coisa e derivada é outra?
09 de Abril de 2015, 10h55
Mensagem de Vitor Nunes
Olá Fernanda,
A Taxa de Variação Média num intervalo, não é mesma coisa que derivada. Mas se estiveres a falar da T.V.M. num ponto, então sim, é a mesma coisa que derivada. Esta taxa serve para "medir" a variação da função num ponto. Por outras palavras, imagina um corredor a cortar a meta, qual a velocidade a que ele ia, no preciso instante em que cortou a meta? A resposta a esta pergunta é obtida pelo cálculo da derivada no instante em que o corrredor cortou a meta.
10 de Abril de 2015, 10h59
Mensagem de Filipa
Bom dia,
Gostaria de saber se irão colocar brevemente alguma aula sobre interpretação geométrica da derivada de uma função num ponto e da função derivada.
Obrigada
10 de Abril de 2015, 14h22
Mensagem de Vitor Nunes
Olá Filipa,
Infelizmente, para já estamos sem tempo para acrescentar novas aulas. Só daqui a duas semanas é que prevejo que voltemos a acrescentar novas aulas para o 11º ano.
20 de Abril de 2015, 18h36
Mensagem de Leandro
Boas,
Pela última mensagem da Filipa, consegui perceber que ainda vai demorar um pouco até o vídeo com a próxima matéria vai sair. Gostaria de saber se tem alguma data prevista para tal, já que tenho de fazer umas revisões para um teste que se avizinha.
Desde já saúdo o vosso esforço para manter este site, é uma verdadeira ajuda para mim e já o recomendei! Muito obrigado
21 de Abril de 2015, 00h28
Mensagem de Vitor Nunes
Olá Leandro,
Ainda vai demorar alguns dias até termos tempo para acrescentar novas aulas. Provavelmente, quando isso acontecer, vamos saltar diretamente para a próxima matéria, que está relacionada com o estudo da Progressão Aritmética e Progressão Geométrica.
Se quiseres, entretanto, podes consultar os seguintes vídeos. Pode ser que sirvam para esclarecer algumas dúvidas que ainda tenhas sobre as derivadas. Boa sorte para o teu teste!
26 de Maio de 2016, 14h52
Mensagem de Ecaterina
Bom dia Professor Vitor.
Tenho uma dúvida. Não percebo quando o declive é positivo e quando é negativo. Podia explicar-me por favor.
27 de Maio de 2016, 09h07
Mensagem de Vitor Nunes
Olá Ecaterina,
O declive de uma reta está relacionado com a sua inclinação. Na equação da reta `y=mx+b`, a constante `m` representa o declive. Este valor pode ser positivo ou negativo. Nesta matéria em que se estuda a Taxa Média de Variação, o valor da TMV é igual ao valor do declive da reta secante nos pontos do intervalo. No estudo da função derivada, o declive da reta tangente é igual ao valor da derivada nesse ponto. Esta constatação é muito importante, porque se o declive for positivo significa que a função é crescente, se o declive for negativo significa que a função é decrescente.
18 de Agosto de 2016, 05h37
Mensagem de vladimir renz
Não estou conseguindo uma definição correta destes termos. Qual é o significado das seguintes relações:
- Taxa de Variação Média e Reta Secante;
- Taxa de Variação Instantânea e Reta Tangente.
18 de Agosto de 2016, 09h47
Mensagem de Vitor Nunes
Olá Vladimir,
A Taxa de Variação Média (TVM) de um função num intervalo é igual, ou seja, tem o mesmo valor que o declive da reta secante nesse intervalo. A Taxa de Variação Instantânea (derivada) de um função num ponto é igual ao declive da reta secante nesse ponto. Todos estes conceitos estão relacionados e percebem-se mais facilmente quando se analisa o gráfico de uma função. Espero ter ajudado!
15 de Dezembro de 2016, 00h29
Mensagem de João Cunha
Acha que me pode explicar as seguintes duvidas:
- qual a relação entre taxa de variação e derivada de uma função.
- como determinar a equação da reta tangente de uma função num ponto de tangencia.
Obrigado pelo esforço que dedicam ao site
15 de Dezembro de 2016, 08h46
Mensagem de Vitor Nunes
Olá João,
Em relação à primeira dúvida, normalmente a Taxa Média de Variação (TMV) de uma função é calculada num intervalo, mas se ao invés de um intervalo for calculada num ponto, então esse valor é igual ao valor da derivada da função nesse ponto. Na segunda dúvida que apresenta, a reta tangente tem como equação `y=mx+b`, sendo que `m` é o declive e corresponde ao valor da derivada no ponto de tangência. Quanto ao `b` basta substituir o `x` e o `y` pelos valores do ponto de tangência.
23 de Maio de 2017, 15h47
Mensagem de Pedro Duarte
Boa tarde
-Poderia explicar a relação entre valores e sinais da derivada e comportamento do gráfico da função
24 de Maio de 2017, 08h30
Mensagem de Vitor Nunes
Olá Pedro,
Tendo em conta que o valor da derivada num ponto é igual ao declive da reta tangente à função nesse ponto, então conseguimos concluir o seguinte: quando a derivada é positiva, a função é crescente; se a derivada for negativa, acontece o oposto, a função é decrescente; por último, se a derivada for zero então nesse local estamos na presença de um extremo relativo da função, que pode ser um máximo ou um mínimo relativo.
11 de Junho de 2017, 23h37
Mensagem de Christophe
Boas, tenho um trabalho para fazer sobre taxa de variação, mas ainda não consegui descobrir quem foi o matemático que a utilizou pela primeira vez e sempre que procuro taxa de variação na internet, aparece sempre é taxa de variação media, são a mesma coisa ou tem diferenças?
será que me podiam ajudar se faz favor?
12 de Junho de 2017, 08h16
Mensagem de Vitor Nunes
Olá Christophe,
Sim, Taxa de Variação e Taxa de Variação Média são a mesma coisa. Quanto ao matemático que a usou pela primeira vez, é mais difícil de responder. Isto porque, muitas vezes as descobertas na matemática vão sendo feitas ao longo de décadas e aprimoradas por diversos matemáticos. Os trabalhos sobre Taxa de Variação estão associados ao aparecimento do cálculo diferencial, cujo desenvolvimento foi feito de forma independente por Gottfried Leibniz e Isaac Newton.
12 de Junho de 2017, 08h46
Mensagem de Christophe
Muito obrigado, estou mais esclarecido.
04 de Maio de 2020, 23h35
Mensagem de Mara Rodrigues
Olá, poderia explicar-me onde se pode aplicar a taxa média de variação. Obrigado.
05 de Maio de 2020, 07h50
Mensagem de Vitor Nunes
Olá Mara,
A taxa média de variação pode ser aplicada em diversos contextos. Vamos supor que está a analisar os lucros de uma empresa referentes a um determinado período de tempo, digamos que três meses. Nesse caso pode ser interessante saber qual foi a variação média dos lucros durante esse tempo. Será que subiu, será que desceu ou não houve variação?

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.








 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 