Primeira derivada e monotonia.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

Já sabes que a derivada de uma função real de variável real num ponto é o declive da reta tangente ao gráfico da função nesse ponto. Se a derivada é positiva em todos os pontos de um intervalo, então a função é monótona crescente nesse intervalo, isto é, os objetos e as imagens variam no mesmo sentido.
Analogamente, se a derivada é negativa em todos os pontos de um intervalo, então a função é monótona decrescente nesse intervalo, isto é, os objetos e as imagens variam em sentido contrário.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
23 de Abril de 2015, 22h03
Mensagem de Tiago Ferreira
Boa noite! No vídeo da resolução do exercício 10, ao min. 17:23 (se não me engano) igualam a derivada a 0,25 apesar de dizerem 0,23. Neste caso não muda o resultado do exercício mas era só para avisar :)
24 de Abril de 2015, 19h03
Mensagem de Vitor Nunes
Olá Tiago,
Tens razão, existe um pequeno lapso na parte final do vídeo, quando se iguala a função derivada a 0,23. Felizmente a resolução nessa parte da questão é feita com recurso à máquina de calcular e esse erro não influencia o resultado final. Em todo o caso, obrigado por reportares. Bons estudos!
18 de Março de 2016, 20h41
Mensagem de Joao Fonseca
Boa noite,
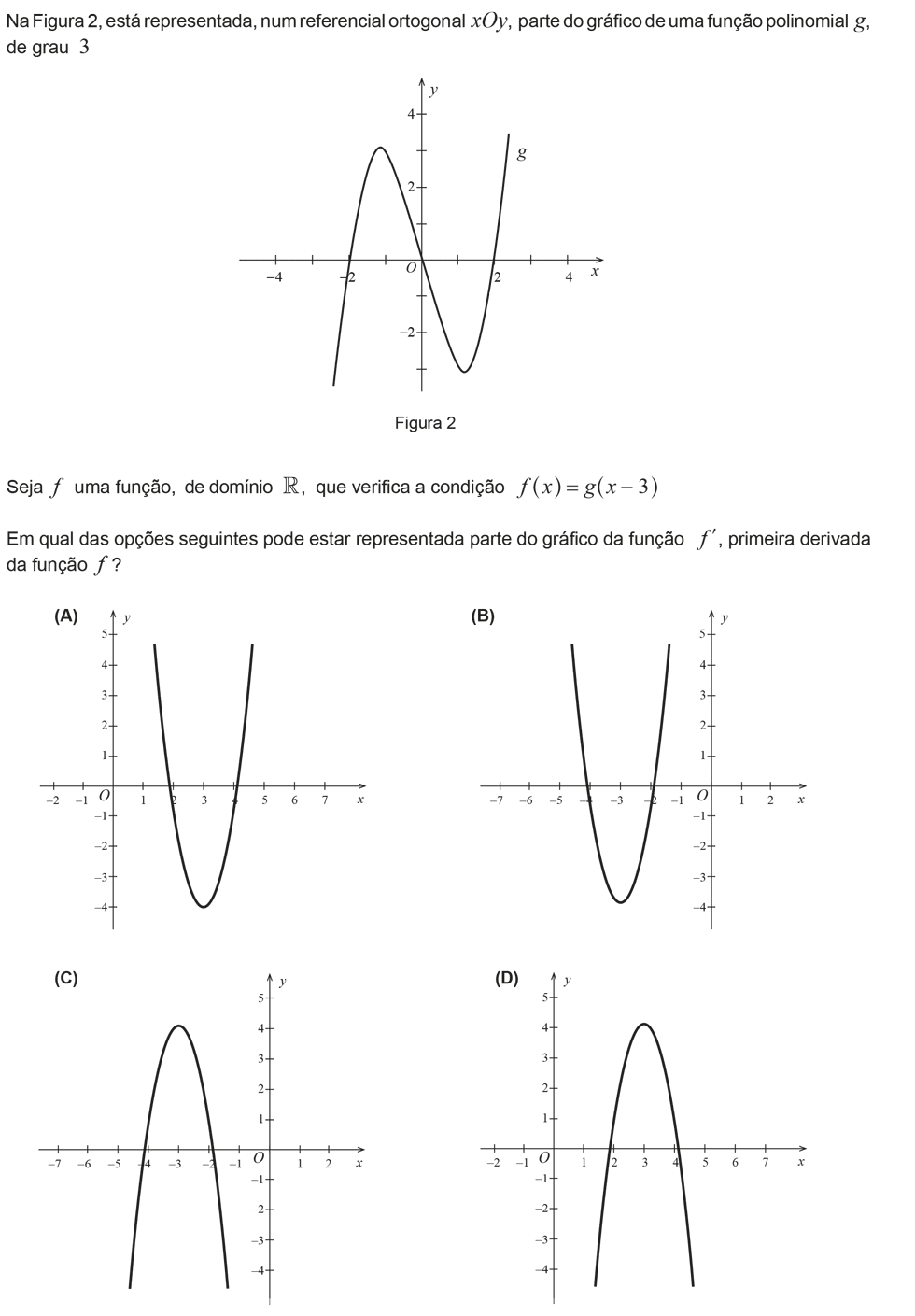
No exercício 6 escreve que o esboço refere-se ao gráfico f(x) mas é o gráfico g(x) já com os devidos deslocamentos
21 de Março de 2016, 09h09
Mensagem de Vitor Nunes
Olá João,
A informação que eu dou no vídeo está correta! Rapara que o gráfico da função `f(x)` corresponde ao gráfico da função `g(x)` após este sofrer um "deslocamento na horizontal" de três unidades. A este "deslocamento" dá-se o nome de translação que neste exercício é feita no sentido de um vetor com as coordenadas `(3,0)`, que vulgarmente designamos com sendo uma deslocação para a direita de três unidades. Espero que tenhas ficado esclarecido.
11 de Abril de 2016, 17h08
Mensagem de Catarina
Olá!
Não percebo como derivar no exercício 7, na regra de derivação do quociente?
12 de Abril de 2016, 13h06
Mensagem de Vitor Nunes
Olá Catarina,
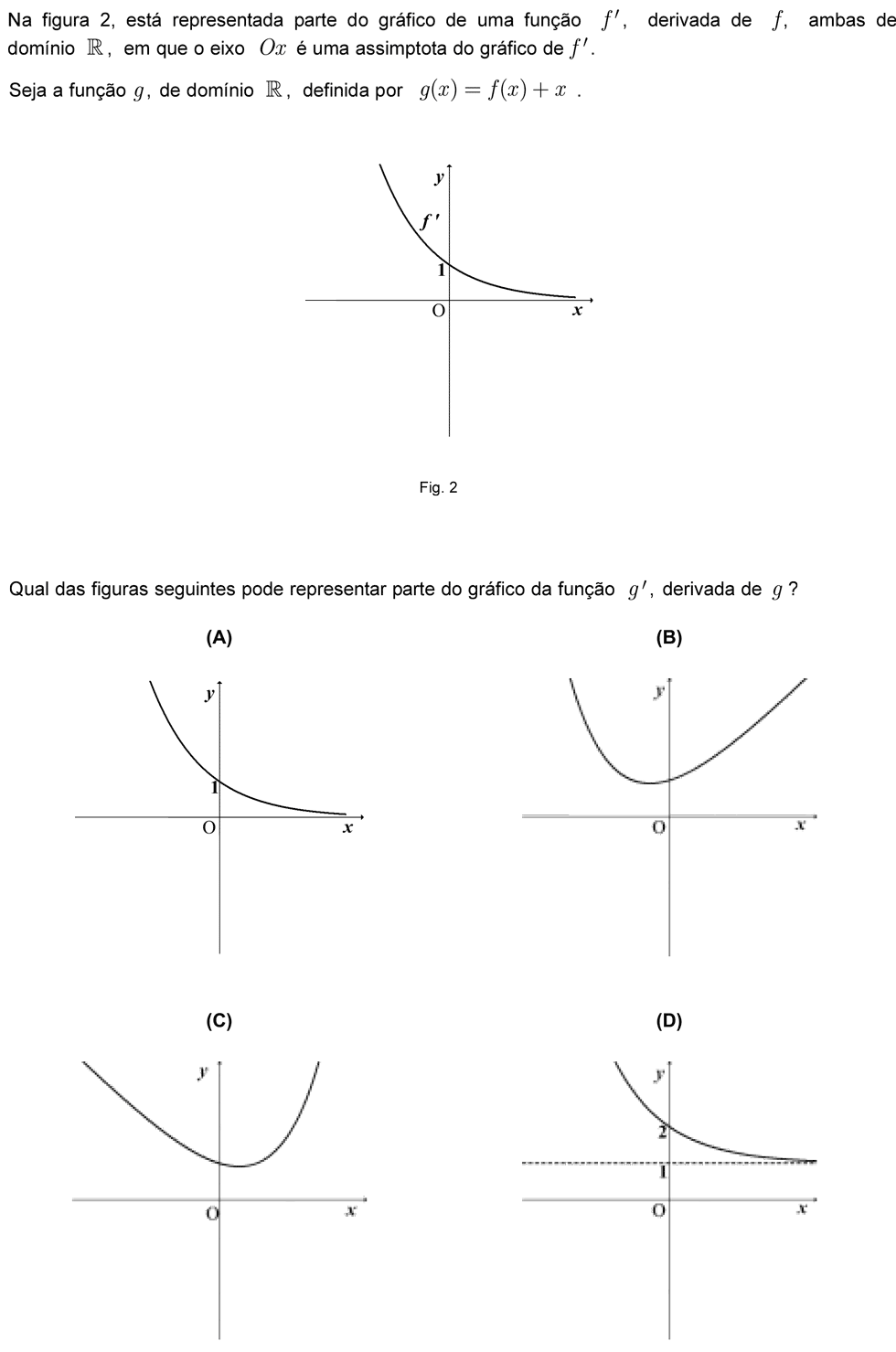
Quando estamos a calcular a derivada de um quociente de funções, utilizamos a seguinte regra: `(u/v)'=(u'v - uv')/v^2`. No entanto, no caso do exercício 7, não estamos a derivar duas funções, mas sim a derivar o quociente de uma constante por uma função. Poderíamos aplicar exatamente a mesma regra, mas isso seria mais trabalhoso, porque para estes casos, existe uma regra mais simples que é a seguinte: `(k/x)'=-k/x^2`. No vídeo com a resolução foi utilizada esta última regra.
20 de Abril de 2016, 22h20
Mensagem de Catarina
Ok, obrigada pelo esclarecimento.
Já agora, no exercicio 9.3, nas assintotas verticais, se um limite dá mais infinito porque é que vamos calcular o outro limite se sabemos que a assintota existe. É obrigatório apresentar os dois limites?
21 de Abril de 2016, 09h04
Mensagem de Vitor Nunes
Olá Catarina,
Quando estudamos a existência de assintotas de uma função, o objetivo é saber como é que a função se comporta quando se aproxima desses pontos, sejam eles pontos de descontinuidade, no caso das assintotas verticais, ou do mais ou menos infinito no caso das assintotas não verticais (obliquas e horizontais). Se o objetivo é apenas concluir a existência ou não de assintotas, então tens razão, não é necessário estudar o comportamento à esquerda e à direita dos pontos.
30 de Abril de 2021, 10h25
Mensagem de Juliana
Bom dia,
No vídeo, aproximadamente aos 17 minutos, no estudo para determinar o intervalo em que a função é crescente e decrescente, não percebi porque razão, o intervalo de x1 e x2 são fechados, tanto para quando a função é crescente como decrescente? Se x1 é fechado quando a função é crescente, como pode ter intervalo fechado quando a função é decrescente (mesmo raciocínio vale para x2)? Ser fechado não implica dizer que o x1 pertence ao intervalo? Estou muito confusa.
Obrigada desde já.
30 de Abril de 2021, 17h02
Mensagem de Vitor Nunes
Olá Juliana,
Por norma, quando indicamos o intervalo de monotonia de uma função, indicamos com intervalos fechados (a não ser que se trate de infinito, ou de um ponto que não pertence ao domínio da função). Isto porque a função cresce até chegar àquele ponto. Da mesma forma, também podemos interpretar que a função decresce até chegar àquele ponto, logo o intervalo é fechado tanto no intervalo de crescimento como no de decrescimento, mesmo que se trate do mesmo ponto.
05 de Maio de 2021, 18h22
Mensagem de Juliana
Boa tarde, Professor.
No exercício 4, resolvi de outra forma e gostaria de saber se está correta. Como os zeros da função são conhecidos, consegui encontrá-la, através da multiplicação dos fatores (x+2) (x-2) (x-5), ou seja, a função é x^3 - 5x^2 - 4x +20. Depois, encontrei a função derivada, que é 3x^2 - 10 x - 4. Por último, substitui os valores de 0, -3 e 6 na função da derivada.
Obrigada.
05 de Maio de 2021, 19h21
Mensagem de Vitor Nunes
Olá Juliana,
Ena, esta certo. Mas tens que concordar que é um processo muito mais trabalhoso. O mais fácil é mesmo interpretar o gráfico da função dada e, a partir da informação que temos tentar descobrir qual é o gráfico da primeira derivada. Em todo o caso, parabéns pelo raciocínio, está corretíssimo.

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.


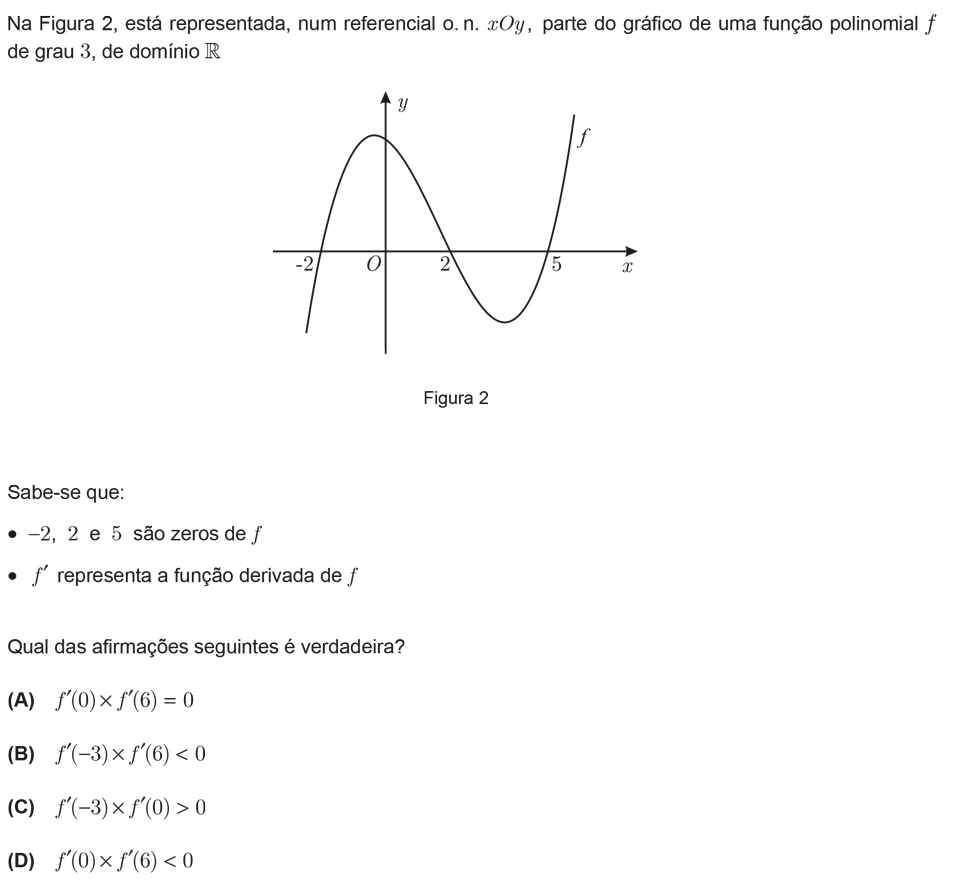








 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 