O número `i`, a unidade imaginária.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

Foi o grande matemático Leonhard Euler que introduziu pela primeira vez a notação `i`, a chamada unidade imaginária, para representar o número `sqrt(-1)`. No seu livro Elementos de Álgebra, Euler refere o seguinte: “… somos levados à ideia de números que são impossíveis pela sua própria natureza, e que, portanto, são habitualmente designados por quantidades imaginárias …”.
Estava, desta forma, aberto o caminho para o conhecimento de um novo conjunto de números, o conjunto dos números complexos, representado por `CC`. Esta nova ampliação do conceito de número, tal como as anteriores, foi feita de acordo com o chamado principio da conservação das propriedades formais do cálculo, ou seja: as novas definições de igualdade, adição e multiplicação conservam, tanto quanto possível, as propriedades formais válidas em `RR`, o que quer dizer que se aplicadas a números reais, coincidem com as anteriores definições.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
02 de Agosto de 2017, 20h22
Mensagem de Rita Vieira
Olá,
Isto não é bem uma dúvida, mas tal como em outros assuntos da matemática, não consigo perceber para que servem os números complexos. Durante anos, aprendemos que as raízes quadradas não podem ser negativas. De repente, aparecem estes números complexos e já podemos calcular raízes negativas. Mas afinal, qual é a utilidade disto?
03 de Agosto de 2017, 09h23
Mensagem de Vitor Nunes
Olá Rita,
Eu sei que por vezes os programas são tão extensos, que não há tempo para explicar aos alunos como é que os conceitos surgiram. Repara que na primária, também te ensinaram que não era possível fazer a seguinte operação: `5 - 7`. Realmente, naquela altura, não fazia sentido, se eu só tinha 5 laranjas, como é que podia dar 7? Só mais tarde é que os números negativos foram introduzidos e isso permitiu-te resolver uma série de novas equações. Em relação aos números complexos, estes apareceram para que fosse possível solucionar equações de terceiro grau, que tinham solução, mas que apresentavam raízes negativas. A noção de número foi evoluindo, os nossos antepassados só conheciam os números naturais, porque só precisavam disso para saber quantas ovelhas tinham. Hoje em dia, isso já não é suficiente, a ida do homem à lua, por exemplo, só foi possível graças a complexos cálculos matemáticos. A aprendizagem dos alunos é feita por etapas, não se pode ensinar tudo ao mesmo tempo!

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.
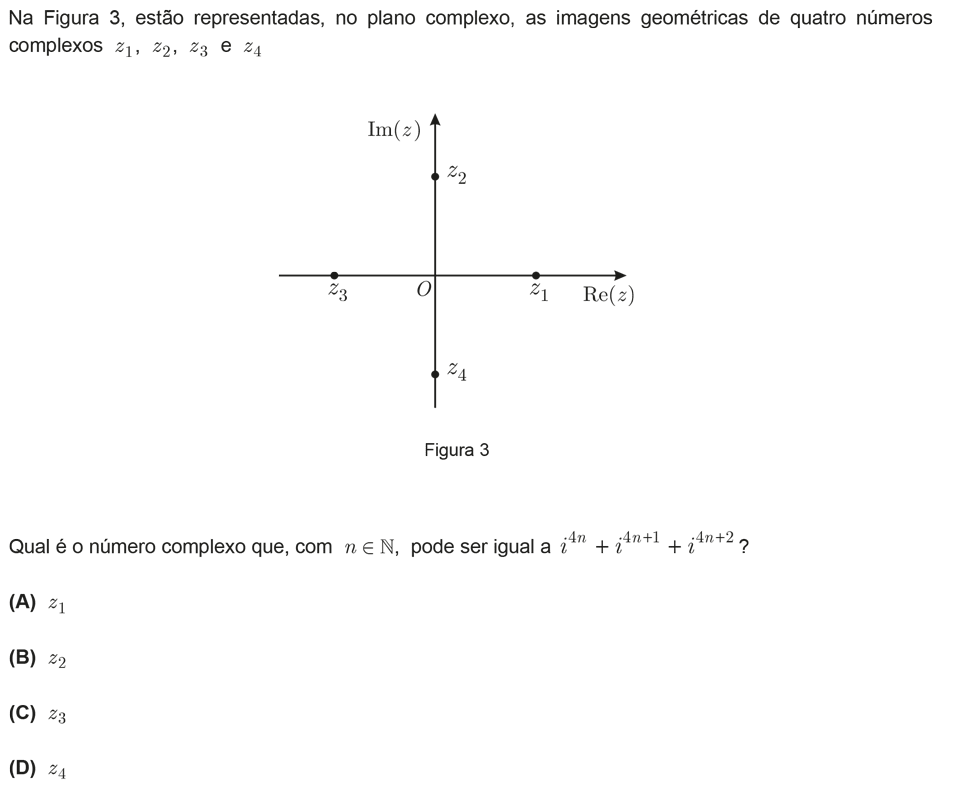


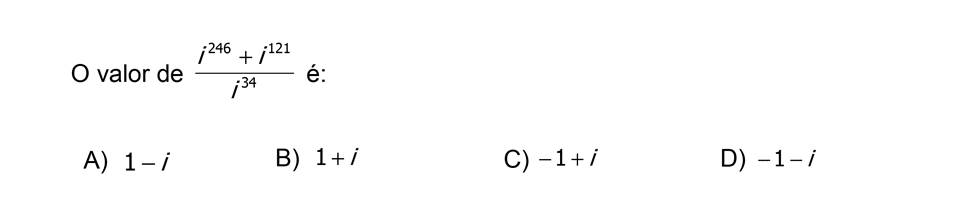

 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 