Monotonia de uma sucessão.

Vê com atenção o vídeo que contém a explicação da matéria. De seguida, imprime a ficha de trabalho e tenta resolver o máximo de exercícios que conseguires sobre este tema. Se tiveres alguma dúvida nos exercícios que disponibilizamos, consulta a resolução proposta ou coloca uma questão no fórum. Bom estudo!
Introdução

Tal como enunciamos para as funções de variável real, também uma sucessão é crescente quando os objetos e as imagens variam no mesmo sentido, ou seja, quando a ordem aumenta, o termo também aumenta. Assim sendo, uma sucessão é monótona crescente, sempre que cada termo é maior que o anterior. É monótona decrescente quando cada termo é inferior ao anterior.
Se é verdade que basta encontrar um contraexemplo para garantir que a sucessão não é monótona e se também é verdade que a calculadora pode dar alguma ajuda, também é verdade que é preciso saber procurar no «lugar certo», o que nem sempre é fácil. Por outro lado, tratando-se de uma sucessão monótona, os exemplos não servem como prova. Não é possível verificar, para todos os termos, se estão sempre a aumentar ou a diminuir, uma vez que o conjunto dos números naturais é um conjunto infinito. Vamos estudar a monotonia através do estudo do sinal da diferença entre dois termos consecutivos, quaisquer, da sucessão.
Explicação da matéria
Exercícios resolvidos
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Nível:
Utiliza este espaço para comentários ou dúvidas
Neste local poderás colocar os teus comentários e as tuas dúvidas. Todas as mensagens que não estiverem diretamente relacionadas com este tema, ou que eventualmente contenham linguagem considerada imprópria serão removidas.
13 de Março de 2016, 11h43
Mensagem de Bernardino Quimino
Como calcular uma sucessão monótona, isto é, em todos os casos?
15 de Março de 2016, 09h22
Mensagem de Vitor Nunes
Olá Bernardino,
Para averiguar a monotonia de uma sucessão, normalmente faz-se o estudo da diferença entre um termo e o termo anterior, isto é, calcula-se `U_(n+1) - U_n`. Se a partir daqui conseguirmos concluir que o seu valor é maior que zero então a sucessão é monótona crescente, caso seja inferior a zero a sucessão é monótona decrescente e se for igual a zero é uma sucessão constante. Se não conseguirmos chegar a nenhuma destas conclusões é porque não é monótona.
21 de Maio de 2016, 20h46
Mensagem de Sofia
Através do vídeo, consegui perceber que para a sucessão ser monótona tem de ser sempre ou crescente ou decrescente e quando é não monótona é porque umas vezes cresce e outra decresce e vemos isso substituindo o n por números naturais, mas não conseguimos fazer isso para todos. Portanto há outra maneira de fazer ou só recorrendo à tentativa? Desde já obrigada e parabéns pelo excelente trabalho.
22 de Maio de 2016, 08h42
Mensagem de Vitor Nunes
Olá Sofia,
Claro que se pode provar que uma sucessão não é monótona calculando alguns dos seus termos e verificar que por vezes "cresce" e por vezes "decresce". O problema é que a sucessão pode ser crescente ao longo dos 50 primeiros termos e no termo de ordem 51 começar a decrescer. Obviamente que o aluno não pode estar a calcular todos os termos para verificar isso. A resposta do comentário anterior explica claramente qual é a única forma de averiguar a monotonia de uma sucessão. Boa sorte!
22 de Maio de 2016, 11h52
Mensagem de Maria
Como estudamos a monotonia de uma sucessão com expoente n?
23 de Maio de 2016, 09h11
Mensagem de Vitor Nunes
Olá Maria,
Da mesma forma que as restantes. Isto é, calcula-se o `u_(n+1)` substituindo o expoente `n` por `n+1`. De seguida, normalmente separa-se a potência com base na regra da multiplicação de potências com a mesma base, para se poder simplificar. Tomemos como exemplo: `u_n = 2^n`, logo `u_(n+1)=2^(n+1)`. Seguidamente, faz-se: `u_(n+1)-u_n = 2^(n+1)-2^n=2^nxx2^1-2^n=2^n`. Como `2^n>0`, conclui-se que a sucessão `u_n` é monótona crescente. Espero que o exemplo tenha ajudado!
11 de Outubro de 2016, 19h37
Mensagem de Maisa Stefany Paris
Como estudar a monotonia de uma sucessao definida por ramos ?
12 de Outubro de 2016, 08h41
Mensagem de Vitor Nunes
Olá Maisa,
O procedimento a seguir nas sucessões definidas por ramos é primeiro estudar a monotonia em cada ramo, como se fossem duas sucessões separadas. Caso exista monotonia e esta seja igual em ambos os ramos é anda necessário fazer um último passo. É necessário verificar o que se passa no ponto de mudança de ramo para garantir que a monotonia se mantém. Por exemplo, se a mudança de ramo for no sexto termo, convém verificar o que se passa nos termos de ordem 5, 6 e 7 para ver se a monotonia se mantém.
01 de Janeiro de 2017, 20h47
Mensagem de Catarina
Olá,
Gostaria de saber como se calcula a monotonia de uma sucessão definida por recorrência, por exemplo: U1=2 e Un+1=1/2(Un + 6), para n >= 2.
02 de Janeiro de 2017, 17h14
Mensagem de Vitor Nunes
Olá Catarina,
Normalmente só respondo a questões que estejam relacionadas com os exercícios disponibilizados. Mas, como esta é uma dúvida frequente, vou responder. Se fosse possível, tentaríamos isolar no segundo ramo da sucessão definida por recorrência a seguinte diferença: `U_(n+1) - U_n`. Como tal não é possível, podemos recorrer a uma linguagem menos matemática para justificar que a soma do número 6 ao termo anterior, seguida pela divisão por 2 do seu resultado, vai sempre dar um termo cada vez maior que o anterior. Logo, a sucessão é monótona crescente. Espero ter ajudado!
08 de Fevereiro de 2017, 17h53
Mensagem de João
Boa tarde, como é que se estuda a monotonia de uma sucessão que se obtém por multiplicação de outras duas sucessões? p.e.: "Estuda a sucessão [(Un)(Vn)] quanto à monotonia."
09 de Fevereiro de 2017, 22h14
Mensagem de Vitor Nunes
Olá João,
É difícil dar uma resposta concreta a essa pergunta, porque o estudo da monotonia do produto dessas duas sucessões vai depender do termo geral de cada uma delas. A forma mais simples de proceder, consiste em pensar numa terceira sucessão, que seja igual ao produto das duas dadas, ou seja, `W_n=U_nxxV_n`. A partir daqui, simplifica o termo geral desta nova sucessão e averigua se `W_n` é monótona.
25 de Março de 2017, 13h15
Mensagem de Manuel Guilherme
Se já nos apresenta a sucessão na forma Un+1 - Un como justificamos que a sucessão é monotona?
26 de Março de 2017, 15h06
Mensagem de Vitor Nunes
Olá Manuel,
Se o termo geral da sucessão for da forma `U_(n+1) - U_n` então fica mais fácil a análise da monotonia da sucessão! Basta analisar a expressão e verificar se o seu valor é maior ou menor que zero, e assim concluir imediatamente se a sucessão é monótona crescente ou decrescente. Se pelo contrário, não for possível tirar nenhuma conclusão acerca do seu sinal, então a sucessão não é monótona.
15 de Maio de 2017, 06h38
Mensagem de Cristina
Uma sucessão é
> monótona
>>> monótona crescente
>>>>> monótona estritamente crescente
>>>>> monótona crescente em sentido lato (ou monótona não decrescente)
>>> monótona decrescente
>>>>> monótona estritamente decrescente
>>>>> monótona decrescente em sentido lato (ou monótona não crescente)
> não monótona
E a sucessão constante? É monótona ou não monótona?
15 de Maio de 2017, 08h16
Mensagem de Vitor Nunes
Olá Cristina,
Uma sucessão constante é monótona. De acordo com a definição da monotonia das sucessões, tanto pode ser considerada monótona crescente em sentido lato como monótona decrescente em sentido lato. Mas, normalmente quando falamos da sua monotonia dizemos apenas que é uma sucessão constante.
14 de Janeiro de 2018, 20h45
Mensagem de Carla
Como podemos encontrar o limite de uma sucessão do tipo limite (1+1/3n)expoente 2n
15 de Janeiro de 2018, 08h47
Mensagem de Vitor Nunes
Olá Carla,
Não tenho por hábito resolver exercícios propostos pelos alunos. Por isso, a única ajuda que posso dar é que a resolução desse limite envolve a utilização do seguinte limite notável: `lim_(u_n->+oo)(1 + k/(u_n))^(u_n) = e^k`. Para conseguir isso, é preciso fazer algumas modificações na expressão que está no enunciado, de forma a encontrar uma equivalente, que tenha o denominador da fração igual ao expoente da potência.
28 de Janeiro de 2018, 11h19
Mensagem de Rafael Dinis
Olá,
Como podemos determinar a monotonia de uma sucessão por ramos em que num dos ramos n pertence aos números ímpares e noutro pertence aos números pares? Ou seja, como podemos estudar a monotonia quando não há só um ponto de mudança de ramos?
Obrigado, Rafael
29 de Janeiro de 2018, 08h46
Mensagem de Vitor Nunes
Olá Rafael,
Sem conhecer a sucessão é um pouco difícil dar a resposta. Normalmente esse tipo de sucessão não é monótona. Para provar isso, calcula por exemplo os 5 primeiros termos e assim verificas que a sucessão não é monótona crescente nem monótona decrescente.
04 de Novembro de 2018, 08h54
Mensagem de Paula Maria Gomes
Bom dia!
Para estudar a monotonia de uma sucessão calcula-se sempre Un+1 - Un, independentemente de estarmos perante uma progressão aritmética ou geométrica? Obrigada.
04 de Novembro de 2018, 16h29
Mensagem de Vitor Nunes
Olá Paula,
O estudo da monotonia de uma sucessão não está relacionado com o facto desta ser uma progressão aritmética ou geométrica. Tanto assim é que, se já souberes que estás na presença de um destes dois tipos de progressão, então também já sabes que a sucessão é monótona. Assim sendo, o estudo faz-se com a fórmula que referes, normalmente ainda antes de saber que estamos na presença de uma progressão!
05 de Dezembro de 2018, 19h28
Mensagem de Érica
Muito útil, aprendi em 2 minutos o que não tinha aprendido em 10 aulas. Muito agradecida, continuação de bom trabalho!
08 de Abril de 2019, 15h18
Mensagem de Hadla
Olá! Quando resolver estes exercícios em exames, preciso necessariamente calcular os primeiros termos, ou posso partir diretamente para a diferença entre dois termos consecutivos quaisquer? Obrigada!!
08 de Abril de 2019, 20h32
Mensagem de Vitor Nunes
Olá Hadla,
Depende da pergunta. Se for perguntado se a sucessão é uma Progressão Aritmética, então terás que provar que a diferença entre dois termos consecutivos é sempre constante. Se pelo contrário, o enunciado já afirma que se trata de uma P.A. e apenas pergunta qual é a razão, nesse caso calcula a diferença entre dois termos que te pareçam ser fáceis de obter, seja eles quais forem, desde que sejam consecutivos.
02 de Novembro de 2020, 14h28
Mensagem de Ancha
Olá, boa tarde, primeiro agradecer a ajuda, o material que enviou foi bastante útil, obrigada.
Estou com uma pequena dúvida, gostaria de saber como verificar se um valor X é termo da sucessão?
02 de Novembro de 2020, 16h49
Mensagem de Vitor Nunes
Olá Ancha,
Para verificar se um determinado número é termo da sucessão, basta igualar o termo geral a esse valor. Após isso estar feito obtemos uma equação que temos de resolver em ordem a `n`. Findo este passo, se `n` for um número natural, então concluímos que o valor inicial é termo da sucessão. Caso `n` não seja um número natural chegamos à conclusão que não é termo da sucessão.
15 de Fevereiro de 2021, 20h17
Mensagem de Ceci
Como faço para descobrir o conjunto de minorantes de uma sucessão não monótona?
16 de Fevereiro de 2021, 07h45
Mensagem de Vitor Nunes
Olá Ceci,
Não te consigo explicar exatamente quais os passos a seguir porque cada caso é um caso. Mas basicamente, tens que analisar os primeiros termos da sucessão e tentar concluir se existe algum termo que seja o valor mais baixo da sucessão. Se existir um valor mínimo então todos os números inferiores a esse valor mínimo são minorantes da sucessão.

Todos os vídeos aqui presentes têm por objetivo fornecer ao aluno explicações de matemática online na forma mais intuitiva possível. Todos eles estão disponíveis para consulta através dos canais do YouTube: matematica.PT, Os números da Inês, ExplicaMat, Academia Aberta, Matemática Simples e Matemática no Mocho. Caso encontres algum erro, (por exemplo um vídeo que não funcione ou que não corresponda à explicação do exercício proposto) ou caso queiras dar alguma sugestão de melhoramento, não hesites em nos enviar um email através da página Contactar. Tentaremos dar resposta tão brevemente quanto possível.


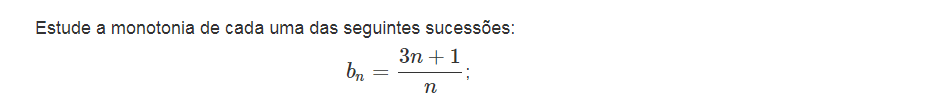




 ATENÇÃO: Para poder utilizar esta opção terá que fazer
ATENÇÃO: Para poder utilizar esta opção terá que fazer 